Let’s go over the basics first. There are various number systems used to count… numbers. Humanity is most familiar with the decimal system, or base10, meaning there are 10 different digits (including zero) used to represent a value for each position of the number. 0, 1, 2, 3, up to 9, before you have to increment the next position and then continue counting. Different bases will just have a different amount of digits used to represent each position of the number.
Counting in binary (base2) goes like: 00, 01 10, 11 …
Counting in quaternary (base4): 00, 01, 02, 03, 10, 11, 12, 13, 20, 21 …
Counting in hexadecimal (base16): 00 … 09, 0A, 0B, 0C, 0D, 0E, 0F, 10 …
And counting in base64 will use the entire English alphabet, both upper and lower case, plus (usually) the characters - and _. Think of it like this: 10 decimal digits + 26 uppercase letters + 26 lowercase letters + 2 auxiliary characters = 64 total digits.
Converting between bases explanation
How do you convert between bases?
Let’s count in binary again.
Observe the times when it moves onto the next position and increments it once.
0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000
Do you notice a pattern?

You need to count twice as much as the previous time before arriving at a new position. You can also say that adding a new position to the number doubled its total capacity. But why double? Because the base of this number system means there’s two digits. The math for this looks like this:
capacity = base ^ position
And we can test it. Say what is the maximum capacity of a binary with 8 places?
capacity = 2 ^ 8 = 256
And to verify, we take the binary 11111111 and convert it to decimal using some online converter:
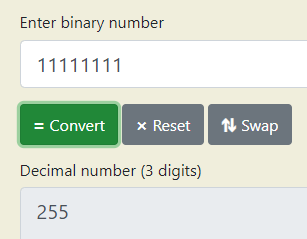
Reminder: Zero is also included, which is why it says 255 and not 256!
Finding the capacity of each position in a specific number system is the basis of base conversion. Because if you know how much each position can store, you know when you should increment the next one, and it lets you formulate the entire number that way.
Now, let’s think of it differently. Instead of each position representing a capacity, say that each position, if it was all alone with no other values, is exactly what value it holds.
10 -> 2
11 --> 3
100 -> 4
111 --> 7
1000 -> 8
1111 --> 15
value = base ^ (position - 1)
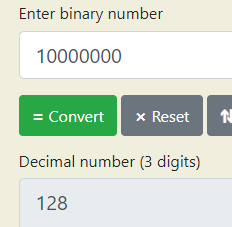
And as an example, the binary number 10000000 where the 1 is at the 8th place:
value = 2 ^ (8 - 1) = 2 ^ 7 = 128
Let’s try it out! We will be converting the decimal number 123 into binary. First, what’s the biggest value of any position that can still fit into 123? It should be 64, which happens to be the 5th place of our number:
01000000
After giving it the 5th place, the remaining number is 123 - 64, which is 59. We then repeat this process, finding the largest position who’s value can still fit into the decimal.
32 = 00100000
59 - 32 = 27
16 = 00010000
27 - 16 = 11
8 = 00001000
11 - 8 = 3
2 = 00000010
3 - 2 = 1
1 = 00000001
1 - 1 = 0
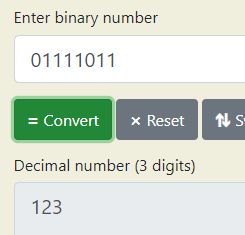
When we combine all these positions into the final number, we get 01111011. We can check if this is correct by converting it back to decimal with the converter tool:
But what if you want to work backwards yourself and convert binary back into decimal? Well, remember the value of each position? If they are filled, that means the value constitutes to the number.
0 1 1 1 1 0 1 1
. 64 32 16 8 . 2 1
If you add all of the values up, 64+32+16+8+2+1, you’ll end up with 123 again.
However, things will get more complicated when you work with higher bases. Let’s now try converting 1234 into a hexadecimal. Now, you’re trying to find the largest number that’s a multiple of the largest position’s value that can still fit into the decimal. Don’t understand? Watch:
First, here are the values of the smallest digits of 4 positions:
4096 256 16 1
The largest position who’s value can still fit into 1234 is the 3rd position.
The value of the 3rd position is 256.
What’s the largest multiple of 256 that can still fit into 1234?
floor(1234 / 256) = 4
256 * 4 = 1024
1234 - 1024 = 210 remainder
The largest position who’s value can still fit into 210 is the 2nd position.
The value of the 2nd position is 16.
What’s the largest multiple of 16 that can still fit into 210?
floor(210 / 16) = 13
16 * 13 = 208
210 - 208 = 2 remainder
The largest position who’s value can still fit into 2 is the 1st position.
The value of the 1st position is 1.
What’s the largest multiple of 1 that can still fit into 2?
floor(2 / 1) = 2
1 * 2 = 2
2 - 2 = 0 remainder, we are done!
We now know that the values of the hexadecimal positions are 4, 13, 2. But these are still in base10 and 13 cannot be represented by a single position! Luckily, you can easily convert these into hex digits since the math have already confirmed that they will each fit into a single position. Many CS students memorize that 13 is the digit D in hexadecimal.
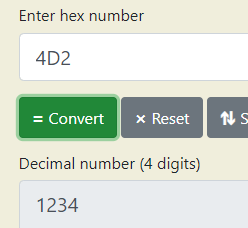
So the final number is: 4D2. And checking it…
And once again, let’s work in reverse on our own.
4 D 2
256 16 1
We have to multiply the digits by their position’s value. Before that, translate each position back into decimal:
4 13 2
256 16 1
Now we multiply:
4 * 256 = 1024
13 * 16 = 208
2 * 1 = 2
And adding them up, 1024+208+2 = 1234.
Coding
We can devise a simple recursion formula to convert decimal into binary. We just need to write the logic with code:
local function decimalToBinary(n)
local largest = math.floor(math.log(n, 2)) --find the largest position that can fit into the number
local result = table.create(largest+1)
for i = largest, 0, -1 do --starting from the largest position:
local value = 2^i --the value of the position
table.insert(result, math.floor(n / value)) --record the number of times that value can fit
n %= value --find the remainder and repeat
end
return table.concat(result)
end
print(decimalToBinary(12345)) --> 11000000111001
In fact, we can get it to convert decimal to ANY base if we provide the digits of that new base:
local function decimalToBase(n, baseDigits)
local base = #baseDigits
local largest = math.floor(math.log(n, base))
local result = table.create(largest+1)
for i = largest, 0, -1 do
local value = base^i
table.insert(result, math.floor(n / value))
n %= value
end
for k, v in result do
result[k] = baseDigits[v+1]
end
return table.concat(result)
end
local hexList = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F',}
print(decimalToBase(12345, hexList)) --> 3039
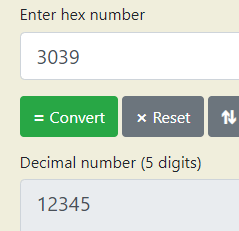
And here’s the way of converting it back:
local function baseToDecimal(n, baseDigits)
local base = 0
local length = #n
for _ in baseDigits do base += 1 end
local result = 0
for i = 1, #n do
local value = base^(i-1)
local position = length - i + 1
local digit = baseDigits[string.sub(n, position, position)] --convert the digit to decimal
result += value*digit
end
return result
end
local hexList = {['0']=0, ['1']=1, ['2']=2, ['3']=3, ['4']=4, ['5']=5, ['6']=6, ['7']=7, ['8']=8, ['9']=9, ['A']=10, ['B']=11, ['C']=12, ['D']=13, ['E']=14, ['F']=15}
print(baseToDecimal('3039', hexList)) --> 12345









