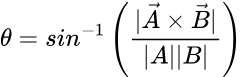Any rotation happens about an axis vector, and by some amount of radians. Using the fromAxisAngle CFrame constructor we can create a CFrame that represents a specific rotation if we know the axis and the angle. It is handy that we can work with the angle separately from the axis, because we don’t actually want to rotate A to face B, we want to rotate a small amount towards B so it eventually gets there, but in a “straight” rotation i.e. always around the same axis. This way we can easily modify the rotation amount independently of the axis.
A is pointing one way, and we want to point it a different way, towards B. So the rotation we want should move the current lookvector (aLookVector) onto the desired one (aToB). We want the rotation to be “straight”, so the axis of rotation should be perpendicular to both the current lookvector and the goal lookvector. Another way to see that the axis of rotation must be perpendicular to both is to look at it from the side. It’s clear that the current and desired lookvectors are in a 2D that is rotated somehow in 3D, and when we rotate something in 2D the axis of rotation is perpendicular to the 2D plane. One property of the 3D cross product is that the resulting vector is always perpendicular to the two input vectors, which is why we use it to get the axis of rotation. Since this axis doesn’t encode any information about the angle to rotate, I just take it to be the unit vector of the cross product. The fromAxisAngle method also only works with unit vectors as the axis, according to the wiki.
As for the rotation amount, it is just a number of radians to rotate. We could use the dot product to compute the angle between the two vectors, but since we already have the cross product for a different purpose we can use that as well. A property of the cross product is that
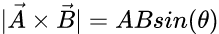
where the left hand side is the magnitude of the cross product. Reorder to solve for the angle and we get
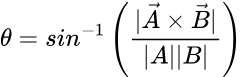
We don’t need the lengths of the vectors to affect the output. After all we’re only talking about directions which should be unit vectors, so let’s work with the unit vectors of A.CFrame.LookVector (already a unitvector) and aToB to construct the cross product. This makes the product under the fraction equal 1 so it simplifies to
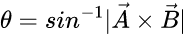
which is what you see in the code. This angle will always be positive, but that’s fine. Rotations in opposite directions is handled with opposite axis vectors.
The reason the axis vector is converted to the object space of the current CFrame of A is that we’re using the * operator to apply the rotation. This operator applies a transform to the left hand side, and when transforms are applied they’re always relative to the existing transform (i.e. the current CFrame). Since the current and goal lookvectors are in world space, the axis of rotation is also in world space. We need to convert it to a vector that is relative to the current orientation of A, whatever it happens to be. VectorToObjectSpace converts a vector from world space to a specific object space, which is just what we need.