Quaternions are numbers which provide a convenient method of describing rotations in 3D space. However, they are not easy to grasp with the mind's eye because they are 4-dimensional, and unfortunately we don't have 4-dimensional eyes to see them with. In this guide I will show several ways to look at quaternions from a simpler perspective.
Why use quaternions?
There are advantages offered by quaternions which other parameterizations of 3D rotations do not have. The most attractive feature of quaternions is that gimbal lock never occurs with them, unlike Euler angles. They are also an excellent analytical tool for the mathematically inclined, as they are an (albeit noncommutative) algebra. Keep in mind though that these benefits are not always necessary when doing rotations in 3D space.
What NOT to use quaternions for- Spherical linear interpolation (AKA Slerp). There are several ways to do Slerp while avoiding quaternions altogether. Stravant has an implementation here.
- Low-DOF systems--if you're rotating through only two axes, then the formula CFrame.fromAxisAngle(v1, alpha)(cf-cf.p)CFrame.fromAxisAngle(v2, beta)+cf.p, where v1 and v2 are axes of rotation, avoids gimbal lock. For Euler angles you can use the CFrame.Angles method instead of fromAxisAngle.
- When 3 or more independent axes of rotation are involved, matrices will always lead to gimbal lock unless one intentionally veers away from singularities in the configuration space. Quaternions, however, may traverse the entire rotation space smoothly with no discontinuities (i.e. gimbal lock).
- Anything involving continuous, nonlinear rotary interpolation will probably involve quaternions in some form. This is because quaternions provide the only continuous parameterization of 3-dimensional rotation space.
Some articles to read Quaternions are a difficult topic, and I recommend you have some background knowledge before taking them on. This article has some very nice interactive visuals describing complex numbers in a straightforward, understandable manner (plus some extra information about Julia fractals!). This is a nice, low-level resource for Euler angles and quaternions discussing gimbal lock and how to avoid it. On the other hand, if you are brave, then this text, while slightly more technical in language, is much more comprehensive than the former. You should have read Trey's guide on vectors. If you haven't, then please do--we're going to be talking about them a lot.
Humble beginnings
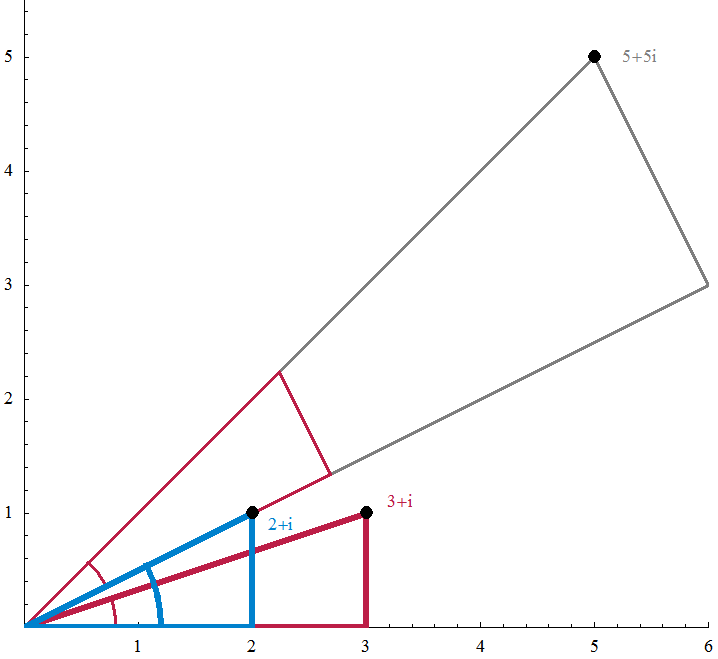
In order to look at quaternions, we'll first examine complex numbers, also known as imaginary numbers. Let's say we have a complex number 
. We can write it in one of two ways:
- Rectangular form:
- Polar form:
. But polar form gives a glimpse at the more fundamental nature of complex numbers. To illustrate -- multiplying two complex numbers adds their angles and multiplies their magnitudes:
It seems far-fetched to think of them as numbers because they don't seem to represent any sort of real-life quantity. Nevertheless, they have all the arithmetic properties of real numbers with the added benefit of being able to perform geometric transformations on the 2-dimensional plane. You can think of complex numbers as an upgrade to real numbers. And while we lose the ability to plot all numbers on a single line (one refers to this as a linear ordering), we gain extra functionality with the complex numbers.
For those of you whoāve taken a course in linear algebra, itās worth noting that complex numbers are superior to 2x2 matrices when combining rotations. While it takes 8 multiplications and 4 additions to multiply 2 rotation matrices, it only takes 4 multiplications and 2 additions via complex numbers. And while using a single parameter to represent the angle avoids these two procedures altogether, quaternions provide an alternative where no linear parameterization exists. Furthermore, the advantage in efficiency is greatly exaggerated in 3 dimensions!
So what are quaternions?
Quaternions can be thought of as the mutant offspring of complex numbers. They also happen to have a bit of an interesting history behind them. They were discovered by a man named William Hamilton. He wanted to extend the complex numbers into three dimensions--that is, find a "larger", number system, with one real component and two "imaginary" components, containing the real & complex numbers. As the complex number system itself is an extension of the real numbers, it is quite natural to wonder if there exist different kinds of numbers beyond the complex horizon.
Hamilton wasn't able to do it in three dimensions, but surprisingly he was able to do it in four. A famous story has it that Hamilton was walking along a bridge with his wife when the solution suddenly occurred to him. He carved the defining equation of the quaternions into the bridge:
i, j, and k are referred to as the basis elements. You can think of them as the x, y, and z axes, respectively. Amazingly, these are the only relations needed to define the quaternions -- if one performs a series of hand-waving manipulations, it is possible to derive some additional identities:
Normally we'd assume that the last statement is a contradiction, since it violates the commutative law of multiplication -- but no such restriction applies to the quaternions. An abstract argument explains why quaternions don't commute: because rotations in 3 dimensions are sensitive to the order in which they are applied, a number system that contains 3D rotations must behave the same way. Thankfully, all the other usual laws of arithmetic hold, so you just have to be a little careful when doing stuff with quaternions. Here's a multiplication table:
So we can see that 1 and -1 commute, while i, j, and k anticommute. Therefore a sum of these numbers will be a mixed bag of commuting elements and anticommuting elements.
Finally, if we use the distributive property, then we can "solve" the equation for quaternion multiplication. Let 
, and 
defined in the same fashion. Then we have
In particular, this means that
The dot denotes not multiplication, but the vector dot product. If you're not familiar with the dot product, read How to think about vectors. The significance of this is that if I take any vector of unit length and "square" it, I get -1. In other words, our imaginary unit lives in 3-dimensional space:
If you paid careful attention, you may have noticed that the real and imaginary parts of the product from earlier are precisely the (negative) dot and cross products of the two vectors from earlier. If we rearrange the equation a little bit, then quaternions can be illuminated as a transformation between two vectors:
Representing rotations with quaternions
Unfortunately for us, quaternions aren't 3D rotations; they rotate through 4-space. The quaternion from earlier is indeed a rotation from 
to 
, but it traverses through 4-dimensional space as it rotates. So actually, the image I provided earlier is not a faithful representation of how quaternions truly rotate.
At this point one must give up their hopes of visualizing quaternions in their entirety (your head just might explode), as humans sadly do not possess 4-dimensional eyes to see with. But as we will find out soon enough, there are in fact ways to examine quaternions in 3 dimensions.
As I said, multiplication by a quaternion will usually will take a 3D vector into the realm of 4D space. Obviously this is not desirable. If we want to rotate in 3 dimensions, we have to use the following formula:
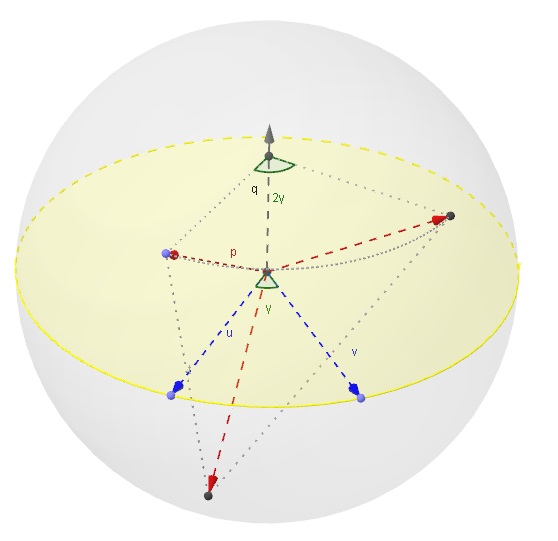
The reasoning behind this formula involves some hardcore abstract algebra which I'd love to talk about--alas, I think my dear readers would be terrified at the prospect. We can instead look at quaternions as rotors, or as double reflections.
Algebraically, the equation for reflecting a vector across another vector is this:
Ā Ā Ā Ā Ā 
Normally quaternion multiplication gets us tangled in 4-dimensional space, but the above equation always lands back in 3D space. The astute reader will know that two reflections makes a rotation ā so, combining two reflections, we arrive at the following equation:
Ā Ā Ā Ā Ā 
One more thing. This equation doesnāt yet quite look how I want it to. Since reflection is its own inverse, swapping āaā with its inverse doesnāt change anything:
Ā Ā Ā Ā Ā 
The last step is not necessary, but it looks nicer and is equivalent anyhow. We say āqā is a rotor.
Thereās a catch to this approach. Rotors rotate by twice the angle between āaā and ābā:
Ā Ā Ā Ā Ā
The great thing about this formula is that we can combine rotations by multiplying quaternions. It takes 27 multiplications and 18 additions to multiply two rotation matrices, but with quaternions it only takes 9 multiplications and 5 additions. This can be summarized by the following tradeoff: rotation matrices are faster at rotating vectors, but slow in composition; and quaternions are slow at rotating vectors, but very fast in composition.
To be continued...
More on quaternions & converting to axis-angle rotations will be here, sometime later.
I know that this is a complicated subject and that not everything may make sense. Iām afraid that this will be the case for some amount of timeāIāve presented a lot of content here. It will take awhile to absorb all of the information.
However if there is anything I can do to help you better understand, i.e. some fuzzy details I left out, please let me know in the replies. Iād be happy to answer any questions you might have
