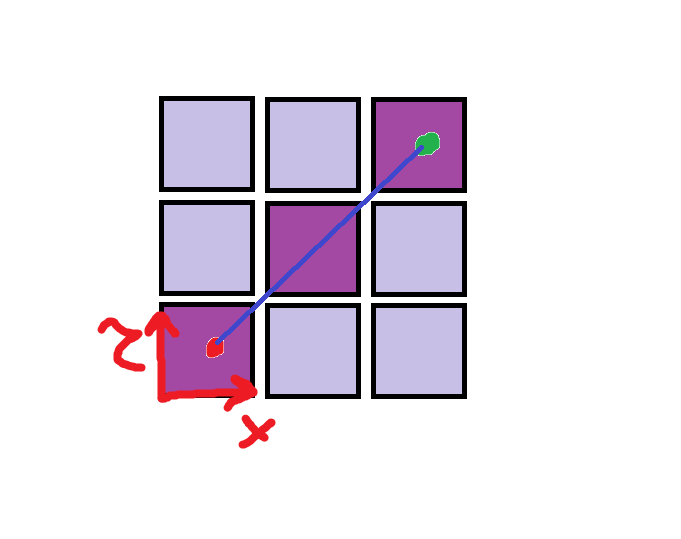
Hello, i worked on this for few hours to help myself in making terrarium game where i’ll be using 3D Grid for my objects, the main idea is that we want to detect all tiles between point A and B, of course in Grids our origin is tile’s corner
Code
If you want to test it, paste it into a folder with 3 parts:
- A
- B
- Origin
local System = script.Parent
--/ Settings
local GridSize = 8
local TileSize = 4
--/ Variables
local GridOrigin = System.Origin.Position
local Grid = {}
--/ Grid Functions
local function visualize(Index: number)
local TileData = Grid[Index]
local Tile = Instance.new("Part")
Tile.Name = Index
Tile.Anchored = true
Tile.Transparency = 0.99
Tile.Color = Color3.new(1,1,1)
Tile.Material = Enum.Material.SmoothPlastic
Tile.Size = Vector3.new(TileSize, TileSize, TileSize)
Tile.Position = Vector3.new(TileData.X, TileData.Y, TileData.Z) + Vector3.new(TileSize, TileSize, TileSize) / 2
Tile.Parent = workspace
TileData.Part = Tile
end
local function generateGrid(Origin: Vector3)
local Index = 0
for y = 0, GridSize - 1 do
for z = 0, GridSize - 1 do
for x = 0, GridSize - 1 do
local X = Origin.X + x * TileSize
local Z = Origin.Z + z * TileSize
local Y = Origin.Y + y * TileSize
Grid[Index] = {X = X, Y = Y, Z = Z}
visualize(Index)
Index += 1
end
end
end
end
--/ Checks
local function isInGrid(Origin: Vector3, Position: Vector3, IsPrinting: boolean)
local Relative = Position - Origin
local x = math.floor(Relative.X / TileSize)
local z = math.floor(Relative.Z / TileSize)
local y = math.floor(Relative.Y / TileSize)
if IsPrinting then print(x,y,z) end
if x > GridSize - 1 or y > GridSize - 1 or z > GridSize - 1 then return end
if x < 0 or y < 0 or z < 0 then return end
return x + (z * GridSize) + (y * GridSize ^ 2)
end
local function detectLine(Start: Vector3, Finish: Vector3)
print("-------------------------------------")
print(isInGrid(GridOrigin, System.A.Position, true))
print(isInGrid(GridOrigin, System.B.Position, true))
print("-------------------------------------")
for i = 1, 100 do
local Lerp = Start:Lerp(Finish, i / 100)
local Index = isInGrid(GridOrigin, Lerp)
local Tile = Grid[Index]
local Visual = Instance.new("Part")
Visual.Anchored = true
Visual.Material = Enum.Material.Neon
Visual.Size = Vector3.new(1,1,1)
Visual.Position = Lerp
Visual.Parent = workspace
if not Tile then continue end
Tile.Part.Transparency = 0.5
Tile.Part.Color = Color3.new(0,1,0)
Tile.Part.Material = Enum.Material.Neon
task.wait(0)
end
end
--/ Callbacks
generateGrid(GridOrigin)
detectLine(System.A.Position, System.B.Position)
Notes:
-
I made grid where origin is lower corner of each tile, you can change that by playing with offsettting grid’s origin
-
I used parts for visual representation, you can remove them if you want
-
You should change Lerp factor to calculation, to make less iterations and overall increase performance
What can i use it for?
Pretty much anything involving 3D grids, the best use scenario for me is while we want to place object in multiple tiles, then we can check which are involved and update their data
I really appreciate feedback and i’m glad i could help you :}