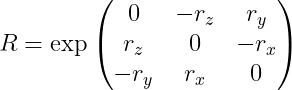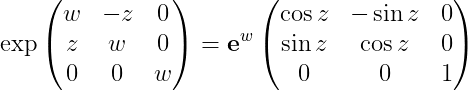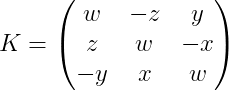Sorry for the late reply, our team has been in the process of moving to Reno.
So I guess my problem with this, now that I know what you mean, is that this conception of RotationVectors does not really play well with existing math.
TL;DR
- Rotation vectors are a linear space, it makes sense to add and scalar multiply them.
- It is not very useful to slerp rotation vectors because they are already in log/angular space; they come about naturally as the logarithm of a quaternion, matrix, or geometric algebraic object.
- There is a very natural and pretty much only one correct way to define slerp, and unitization is not a part of that.
The definition, a * (a^-1 * b)^t, naturally works for non-unit inputs, and guarantees a constant log-angular derivative of log(a^-1 * b), alternatively can be defined as d/dt slerp(a, b, t) = K*slerp(a, b, t), where K is the log of a scaling-rotation matrix.
Uses and linearity
Rotation vectors are typically used to describe angular velocity, including in the Roblox engine, but they are also good at representing changes in orientation angularly, at least in pure math, and are about as accurate as quaternions are. I think we agree on this.
Rotation vectors are a vector space. You can multiply by a scalar and add rotation vectors to get another valid rotation vector.
(Fun fact: A rotation vector in 2D is just a scalar. In 3D, it is a 3-vector. In nD, it is an n*(n - 1)/2 - vector, and become ambiguously ordered!)
- You will scale and add rotation vectors when two spinning rigid bodies collide in space. Roblox does this in their physics engine.
- You can convert rotation matrices to rotation vectors, and add them, to get a rotation vector describing a kind of commutative multiply operation between rotation matrices. Roblox does this to blend animations together.

- You will scale a rotation vector in the process of interpolating rotations. This is the standard “slerp” algorithm for rotation matrices
Conversions to and from rotation vectors
Most of the utility of rotation vectors comes from the fact that they play nicely with rotations.
R is a rotation matrix
Q is a quaternion
r is a rotation vector
Rotation Vector to Matrix
Convert rotation vector to log-rotation matrix and exponentiate:
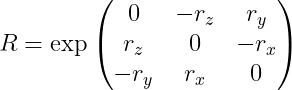
Expanded, this looks like:
Rotation Vector to Quaternion
Convert rotation vector to a pure imaginary quaternion and exponentiate:
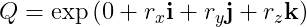
Rotation Matrix to Rotation Vector
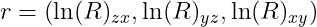
Quaternion to Rotation Vector

If one were designing a RotationVector library, definitely the following methods would be in place:
:ToQuaternion(), :ToLogQuaternion(), :ToCFrame() and :ToLogCFrame(). (The CFrame library would be rewritten to allow for scalar multiplication and addition)
How to slerp with rotation vectors
Because Rotation Vectors are a linear space, you can technically slerp rotation vectors. Though in practice, this tends not to have any real application. It’s like doing a log operation inside of a log operation. Once you are in Rotation Vector space, it makes more sense to linear interpolate them. This is how Roblox blends their animations in a commutative way. However, scaling a rotation vector provides a way to interpolate rotations with a constant angular velocity (which is where “slerp” comes from).
A is a matrix
B is a matrix
t is a scalar interpolation factor
How you would use RotationVectors to slerp a matrix is pretty nice. slerp(A, B, t) is:
- Get the delta rotation matrix between two matrices,
A and B: D = A^-1 * B
- Convert
D into rotation vector, r: r = D:ToRotationVector()
- Multiply
r by t, our interpolation factor: r' = t*r
- Convert back into a delta matrix,
D': D' = r':ToRotationMatrix()
- Multiply
D' back out of A, to get our interpolated matrix, C: C = A * D'
For quaternions, it is similar:
C = A * (t*(A^-1 * B):ToRotationVector()):ToQuaternion()
How to slerp Vector3’s with a Rotation Vector conventionally with Quaternions
a is a vector
b is a vector
t is a scalar interpolation factor
Solution 1: Converting vectors to pure imaginary quaternions
- Take
A and B to be pure imaginary quaternions: A = (w: 0, xyz: a) and B = (w: 0, xyz: b)
- Perform the same process as with rotation matrices as defined above:
C = A * (t*(A^-1 * B):ToRotationVector()):ToQuaternion()
- Convert
C back into a vector
(For fun) Solution 2: Finding a minimal quaternion
- We want to find the angularly minimal quaternion,
Q, which when applied to a will turn it into vector b. We can get double this quaternion, D = Q^2: D = (w: a dot b, xyz: a cross b)
- We can convert the quaternion,
D into a rotation vector, d: d = D:ToRotationVector()
- We can get rid of the doubling by dividing
d by 2: r = d/2
- Now we multiply r by our interpolation factor, t:
r' = t*r
- And now convert back into a quaternion:
Q' = r':ToQuaternion()
- Apply quaternion
Q' to vector a to get our interpolated vector c: c = Q:sandwich(a)
Complications of using rotation vectors for interpolation:
A problem with using rotation vectors for interpolation, both in the quaternion and vector cases, is that you lose some information about scale. You will result in a unit quaternion and a unit vector regardless of the magnitudes of your input vectors / quaternions.
Notice how when converting from a rotation vector to a matrix, we have 0’s in the diagonal. Similarly, we have a 0 w component in the conversion formula from rotation vector to quaternion.
These 0’s come from ln(scale), when the scale is 1 (ln(1) = 0)
Look at what happens when we place w in the diagonals of a log-rotation matrix, turning it into a log-scaling-rotation matrix.
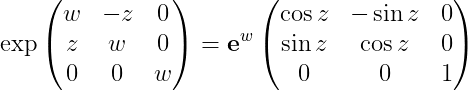
Simiarly with quaternions:
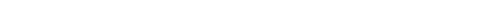
We now include scale information.
We can remove this loss of information by never converting into a rotation vector in the first place:
A * (t*(A^-1 * B):ToRotationVector()):ToQuaternion()
→ A * exp(t*log(A^-1 * B))
→ A * (A^-1 * B)^t
Ultimately…
Defining slerp in this way still satisfies the slerp definition. The interpolation of vector a to b is spherically linear, that is, constant angular velocity (projection of the point onto the unit sphere results in a constant velocity magnitude).
Ultimately, it still generally satisfies c' = K*c, the basic definition of spherical motion. (While linear interpolation of magnitude does not.)
where c = slerp(a, b, t)
and c' = d/dt c
and K is a log-scaling-rotation-matrix, a matrix of the form 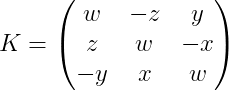
This post is getting too long and is taking too long to write.