[MATH] Max Levelling Algorithm with Huge Amounts of Money

[xeavz (Xea)]

(tl;dr at bottom if you hate maths)

Hi All,

Thanks for coming to my post! I am currently developing a system in my game where player’s can upgrade their abilities (e.g., More Money, Lower Cooldown etc.). The premise of the game isn’t too important here, but in the game, players will be able to amass absolutely behemoth amounts of money (up to amounts like 10^1000000).

Each item in the shop has its own cost function which takes in the current level of that upgrade and returns the amount of money that it would take to upgrade it. For example, this is the cost function for cooldown, where C(x) is the cost to upgrade at a level x:

To avoid players with enormous amounts of cash repeatedly clicking upgrade (perhaps even forever), it’s essential that a “Max Upgrade” button is included to automatically max out the level given the player’s money. This is where the problem comes in.

For a max upgrade button, it seems that I have to calculate the series for every function for every item in the shop individually (which is a lot of series), and it seems to be that any method for determining how many levels a user can buy is extremely inefficient. I’m going to spare the details, but it’s in theory possible to calculate the series for any function like this, then use Newton-Raphson on it to get the maximum possible purchasable levels. However, because some of my functions can have extremely large gradients, Newton-Raphson barely moves and it can sometimes, with huge values, take millions if not billions of iterations to get the correct number of levels that the user can buy. Terrifying .

I’ve recently scrapped trying to use the aforementioned series method. Instead, I have tried to unify the max levelling algorithm under a singular function, and thought about using Riemann Sums / other similar methods to approximate a series given a cost function. I’ve unfortunately had a hard time implementing this. Even if I could approximate these series I would still have to approximate how many levels the user can buy using Newton-Raphson, which as explained earlier is something I just can’t do.

I’m honestly not entirely sure what to do, I’m thinking about changing this system to just avoid this problem altogether. I also know that I can make use of inverse functions if I make my functions less crazy. I have also found this Wikipedia Page on root-finding algorithms that might help me replace Newton-Raphson, but I don’t think any stand out to me.

tl;dr players can have huge amounts of money to buy upgrades, need a max levelling algorithm to find the amount of levels a player can buy given their money. each upgrade has a different cost function, want to just put it all under one max level calculating function. ideally want methods for series approximation and something other than newton raphson (because large gradients of functions) to find how many levels a user can afford.

Any help is greatly appreciated

Thanks!

[KJry_s (MalleoZephyris)]

This is not really a math problem, more like a scripting problem.

First to get the cost of the next upgrade you use the formula you gave us.

Cost = .3(Level + 1)^5 + 20

Now what we have to do is get the player’s money

local Money

Now we have to do a loop to keep checking if they have enough money.
I do not suggest to use a while loop as this could go on for ever.

local TotalCost = 0 -- Cost
local UpgradeLevel = level -- The cost is for this level, which is the highest they can buy

for currentLevel = level, (level + 10) do -- loops 10x
   local Cost = .3(currentLevel + 1)^5 + 20
   TotalCost += Cost -- Add the values together

   if Money >= TotalCost then
       -- Can buy the next level
      UpgradeLevel = currentLevel
   else -- Stop looping if you cant get the next level
      break
   end
end 

[xeavz (Xea)]

The amount of levels that a user can buy can often be huge, and unfortunately I can’t iterate through each level to see if the user can buy each one. Thank you for your response, though!

[KJry_s (MalleoZephyris)]

I mean you could insert the cost and get the level always.
I’ll edit this post once I found the solution for that.

If we reverse the formula it would become:

C = .3(L + 1)^5 + 20
C - 20 = .3(L + 1)^5
(1/.3)(C - 20) = (L + 1)^5
((1/.3)(C - 20))^(1/5) = L + 1
L = ((1/.3)(C - 20))^(1/5) - 1

Now this will be the max level they could buy if we ignore the other costs.
And because the costs becomes exponentially bigger, we can loop backwards instead of forwards like we just did. Most likely you will only need to loop once again, but this can be a point which you can use to get near the Level you can buy.

[PerilousPanther]

You could probably decrease the computing power of any solution by reducing the amounts of money your players can have - is there any particular reason why you want such large amounts? Realistically any meaningful operation on 10^1000000 would require massive amounts of resources. There’s a reason why the biggest possible number you can use with vanilla lua is significantly less than that.

Having said all that, the best way to find the maximum combined cost using maths would probably be to integrate from (max - current) to (max):

This would give every cost of every level between max and current.

However, I don’t know how you would go about calculating the max value when you’re working with what is essentially an exponential function and numbers so big. The only suggestion I can make is that you approximate what could be near the max and then work backwards using some kind of searching algorithm of sorts. Maybe find the max in chunks? Get a large max, then decrease by 20 levels, check if higher or lower, then 10 levels etc.

edit: I think you might actually be able to get the max by getting the integral and making it equal the money they currently have, then finding x. I can’t remember if you have to include the constant of integration in these kinds of problems. It would make it a lot simpler if not.

[xeavz (Xea)]

Yeah I’ve thought about this, I’m currently trying out a similar method to this where I am using trapezia to estimate the cost between xstart (player’s starting level) and some other value I need to find using the player’s currency. I’ll post updates here if it gets anywhere.

[xeavz (Xea)]

I figured out a way to do this a couple days ago and I’m adding my solution here just in case anyone has a similar issue.

Long story short, I am no longer using sums to get an exact estimate for the number of levels a user can buy, and to use simpler equations (sort of). Let me explain:

My previous system would try to generalise the summation for an equation, one of which being the one in the first post I made here, resulting in a rather nasty sixth degree polynomial that I needed to solve the roots of (not very nice). But the nice part would be that I could model cost discretely instead of continuously, so cost would be much nicer to look at.

The Solution

Anyway, I have since changed my system, so instead of using sums, I use integrals. So, instead of solving for n in something like this:

I am now solving for n in something like this, where S is the StartingLevel that the upgrade was at initially (note the continuity correction), and n is the number of levels that the user can buy:

(I only use the formula above for polynomials because other formulas like exponentials have their own series)

Example

In my first post I gave the example 0.3(x+1)^5+20. However, for simplicity in calculating I have removed the +20 because it becomes irrelevant for large values (of which I mostly work with)

The cost at each level for this formula would be:

Of which you can just manually calculate the integral of (using chain rule, or however you would like to calculate it with your own functions) and substitute in the bounds.

In code, this would look something like:

function GetCostAtLevel(Level)
	local function Bound(x)
		return ((x + 1) ^ 6) / 20
	end
	return Bound(Level + 0.5) - Bound(0.5)
end

Now here comes the fun part, calculating max level, but with this method it’s much easier than using Newton-Raphson a trillion times (thankfully). Recall how to solve for the cost between a StartingLevel and an EndLevel. Let’s rearrange this formula for n, so that we get a function for n in terms of S (starting level) and C (currency).

We know that the integral (cost) evaluates to this:

Hence, by substituting the bounds into the equation, you can write this as:

Multiplying both sides by 20 and moving (S+0.5)^6 to the other side of the equation:

Sixth rooting both sides:

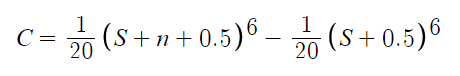
Moving (S + 0.5) to the other side of the equation results in an equation for n, the maximum number of levels the user can buy, hooray! You can floor this to get the integer value for the max levels:

This is that exact same equation in code, it takes parameters StartingLevel and Currency, which are S and C respectively:

function GetMaxPurchasableLevels(StartingLevel, Currency)
	return math.floor(math.pow(20*Currency + (StartingLevel + 0.5)^6, 1/6) - (0.5 + StartingLevel))
end

Remember that this is just the formula for n for one function! You can use this for any (mostly polynomial) function you want, just follow the method above. Also linking back to the initial post, you can use this with Bnum to solve with huge values of C, S and n.

This is pretty much the only way you’d want to tackle this problem with high degree polynomials. One of my older solutions still involved using sums on a function, then using the quadratic or cubic formula to solve exactly for n. However, this means that you’d be limited to only using linear or quadratic functions for your cost, which was not ideal for me. In theory you could also use a cubic cost formula and use the quartic formula on the sum to solve for n, but that’s just really, really awful to implement and I really don’t recommend it at all (especially with Bnum, seriously, the amount of times I had to type Bnum because it’s a module got me like ).

That’s pretty much it. I mostly typed this out for myself so I remember what to do, but I hope at least one person gets some use out of this.