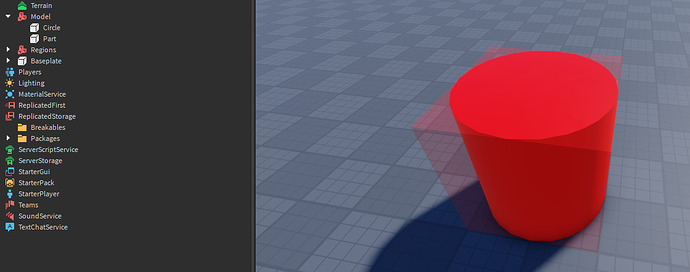
Hello! My name is @Milkeles and in this tutorial I’ll show you how you can generate points that are randomly distributed without having them overlap.
WHO’S THIS TUTORIAL FOR AND WHY IS IT USEFUL?
Before you read this tutorial you should have good knowledge of the syntax in Lua and have at least basic understanding of time and space complexity analysis, and understand object-oriented programming (optional, you’ll probably understand the code regardless, but I’ve written some of it that way because it’s for my own game)
This tutorial was inspired by The Mad Murderer X by @loleris but a few other games I’m aware about, such as the pet Simulators by Big Games and Murderer Mystery 2 also generate objects at random locations for similar purposes - loot/coins. While I do not know what algorithms any of them implemented to achieve that, I will propose a few and go over the advantages and disadvantages of using each one. Of course, these algorithms can also be used for procedural generation of things other than coins, such as trees in a forest. Keep in mind, though, that there are other algorithms that I’ll not cover in this tutorial and different ways to implement the ones I’m using.
RANDOM / REJECTION SAMPLING
The first and least efficient algorithm to achieve the desired result is called random sampling. It is very simple - you generate a point at a random location within some area. Then, to ensure that it does not overlap with other points in the area, you can do one of the following things:
- Check if it collides with any other points. If it does, delete it and attempt to generate a new one.
- Set some default minimal distance between points. For each generated point check if the distance from the generated point to all other previously generated points is greater than the minimal distance. If not, generate a new point.
The second way is what you do when you want the points to not overlap and also be evenly distributed.
- When to and when not to use this algorithm?
Random sampling is a straightforward and intuitive method for generating points, but it may not always provide optimal results, especially in terms of uniformity and efficiency. It is useful when you want to generate a small amount of points within an area but it quickly becomes dangerous if you do not limit the amount of attempts and/or points you want to generate. Because of its random nature, it may end up infinitely attempt to generate points even if the area is not too small or the amount of points you wish to generate is not too huge. Even so, it is still the best solution for the majority of cases especially if you prevent the possibility of unlimited attempts to generate points.
Here’s an example function of how you’d use Random Sampling checking only for collisions:
local minimalDistance = 5
function RandomPoint.new(area, existingPoints)
local self = setmetatable({}, {__index = RandomPoint})
-- Create a part to visualize the point
self.Part = Instance.new("Part", workspace)
self.Part.Anchored = true
self.Part.Name = "Part"
self.Part.Size = Vector3.new(1, 1, 1)
local originCFrame
-- keep checking repositioning the part until a suitable position is found.
-- Note: Not limited by attempts or max parts, therefore, it will crash.
repeat
-- Generate random x, y position within the spawn area
originCFrame = area.CFrame * CFrame.new(
math.random(-area.Size.X/2, area.Size.X/2),
0,
math.random(-area.Size.Z/2, area.Size.Z/2)
)
self.Part.CFrame = originCFrame
until self:checkDistanceFromPoints(existingPoints)
return self
end
-- check all existing points to ensure their distance to the point is greater
-- than the minimal one.
function RandomPoint:checkDistanceFromPoints(existingPoints)
for _, point in pairs(existingPoints) do
local distance = (point.Part.Position - self.Part.Position).Magnitude
if distance < minimalDistance then
return false
end
end
return true
end
QUADSIRANDOM SEQUENCES
This may not be the most accurate definition, but to explain them simply, quadsirandom sequences, also called a low-discrepancy sequences, are simply sequences of numbers generated by math equations. What’s different between them and purely random distribution of points is that if we use indices to generate them, we can easily tell where the next or previous point will be by incrementing or decrementing the index. Please note that quadsirandom sequences create a pattern that is seemingly random, but not purely random and they do not prevent points from overlapping but they’re far more unlikely than when you place points at random places and depending on the specific use case they can provide satisfying results more efficiently than the random sampling. There are many quadsirandom sequences, it’s up to you which one you decide to use but I will use the Halton sequence for the sake of this tutorial. To put it simply, you can generate many seemingly random points efficiently without the risk of crashing your pc and as long as the area is not too small or has too many points in it, collisions are very unlikely (but not impossible). Unlike the previous algorithm that is random, and thus unpredictable, for this one using the Halton sequence I can tell that its worst time complexity is O (n * log n). You can check out the equation for the sequence itself but since this is not an algorithm, there is not much that I can explain, my code is just a calculation using the formula:
local HaltonSequencer = {}
HaltonSequencer.__index = HaltonSequencer
--Create sequencer object, so we can retrieve the index easily
-- not necessary if you don't need the index.
function HaltonSequencer.new()
local self = setmetatable({}, HaltonSequencer)
self.haltonSample = Instance.new("Part") -- Assuming haltonSample is a Part
self.index = 1
return self
end
--Get next point in the sequence and visualize it
function HaltonSequencer:GetNext(area)
-- calculate coordinates and move parts within the area
local x = area.Position.X + (self:Halton(2, self.index) - 0.5) * area.Size.X
--local y = area.Position.Y + (self:Halton(3, self.index) - 0.5) * area.Size.Y -- for 3D
local z = area.Position.Z + (self:Halton(5, self.index) - 0.5) * area.Size.Z
-- create part to visualize the point
local newPart = self.haltonSample:Clone()
newPart.Size = Vector3.new(1, 1, 1)
newPart.Position = Vector3.new(x, area.Position.Y, z) -- for 2D
-- newPart.Position = Vector3.new(x, y, z) -- for 3D
newPart.Parent = game.Workspace
newPart.Anchored = true
newPart.BrickColor = BrickColor.Random()
self.index = self.index + 1
self.t = tick()
-- purely for visualization purposes, not necessary!
spawn(function()
task.wait(10)
newPart:Destroy()
end)
end
-- Function to calculate position from given index
function HaltonSequencer:Halton(b, index)
local result = 0.0
local f = 1.0
while index > 0 do
f = f / b
result = result + f * (index % b)
index = math.floor(index / b)
end
return result
end
return HaltonSequencer
What I personally like about the Halton sequence is that you can easily change it to generate random points in 3D space as well, some other sequences require more changes. Here’s also a script to test it with, although, I suppose this one is simple enough to come up with even without my help:
local HaltonSequencer = require(game.ServerScriptService:WaitForChild("HaltonSequencer"))
local sequencer = HaltonSequencer.new()
while task.wait(0.5) do
sequencer:GetNext(workspace.SpawnArea)
end
Results:
2D:
3D:
As you can see, despite the small area and huge amount of points, there are no collisions between them but the halton sequence itself does not prevent collisions and that the points are not randomly generated, they just seem random, so it is possible that if you increase the amount of points or make the area even smaller a few of them will overlap. Also, unlike the random sampling and the next one, there is no efficient way to ensure even distribution between the points but they’re usually at satisfying distance from one another. Overall, this is easy to implement and gives satisfying results for more points than the random sampling and will work fine unless you plan to spawn a very huge amount of points and/or want them to be evenly distributed.
Bridson’s algorthm (Fast Poisson Disc Sampling)
Fortunately, there’s an efficient and stable algorithm you can use if you do want to spawn as many points as possible and you do want them to be evenly distributed without overlapping. It will use a little more memory than the previous two methods, though, but as you probably know or have noticed there’s always a trade off between time and space complexity, in this case it does not use a significant amount of memory, though. This algorithm is known as Bridson’s algorithm and is overall an improved version of the Poisson Disc Sampling. You can check out a short paper about this algorithm that its creator published here.
Since the paper explains the algorithm very well and there’s a very good popular tutorial in YouTube for Unity, I will not go into details about how it works. I will, though, attempt to make the code similar to the tutorial I linked above despite that my initial implementation was slightly different:
local PoissonDiscSamplingModule = {}
-- Function to generate points using Bridson's algorithm
function PoissonDiscSamplingModule.GeneratePoints(radius, area, numSamplesBeforeRejection)
-- Set a default value for the number of samples before rejection if not provided
numSamplesBeforeRejection = numSamplesBeforeRejection or 30
-- Calculate the cell size based on the specified radius
local cellSize = radius / math.sqrt(2)
-- Calculate the grid size based on the area and cell size
local gridSizeX = math.ceil(area.X / cellSize)
local gridSizeY = math.ceil(area.Y / cellSize)
-- Initialize an empty grid to keep track of points in each cell
local grid = {}
for i = 1, gridSizeX do
grid[i] = {}
for j = 1, gridSizeY do
grid[i][j] = nil -- Each cell initially has no point
end
end
-- Initialize lists to store points and potential spawn points
local points = {}
local spawnPoints = {}
table.insert(spawnPoints, Vector2.new(area.X / 2, area.Y / 2)) -- Start with a center point
-- Main loop for generating points
while #spawnPoints > 0 do
local spawnIndex = math.random(1, #spawnPoints)
local spawnCentre = spawnPoints[spawnIndex]
local candidateAccepted = false
-- Attempt to generate a valid point in the neighborhood
for i = 1, numSamplesBeforeRejection do
local angle = math.random() * math.pi * 2
local dir = Vector2.new(math.sin(angle), math.cos(angle))
local candidate = spawnCentre + dir * math.random(radius, 2 * radius)
-- Check if the candidate point is valid according to Bridson's criteria
if PoissonDiscSamplingModule.IsValid(candidate, area, cellSize, radius, points, grid) then
-- Add the valid point to the list of points and potential spawn points
table.insert(points, candidate)
table.insert(spawnPoints, candidate)
-- Update the grid with the index of the added point
local cellX = math.floor(candidate.X / cellSize) + 1
local cellY = math.floor(candidate.Y / cellSize) + 1
grid[cellX][cellY] = #points
candidateAccepted = true
break
end
end
-- If no valid candidate is found, remove the current spawn point
if not candidateAccepted then
table.remove(spawnPoints, spawnIndex)
end
end
-- Return the generated points
return points
end
-- Function to check if a candidate point is valid
function PoissonDiscSamplingModule.IsValid(candidate, area, cellSize, radius, points, grid)
-- Check if the candidate point is within the specified area
if candidate.X >= 0 and candidate.X < area.X and candidate.Y >= 0 and candidate.Y < area.Y then
-- Calculate the cell indices for the candidate point
local cellX = math.floor(candidate.X / cellSize) + 1
local cellY = math.floor(candidate.Y / cellSize) + 1
-- Check if the cell in the grid has an existing point
if grid[cellX] and grid[cellX][cellY] then
local pointIndex = grid[cellX][cellY]
-- Check if the distance to the existing point is less than the radius
if pointIndex and points[pointIndex] then
local sqrDst = (candidate - points[pointIndex]).Magnitude
if sqrDst < radius * radius then
-- The candidate point is too close to an existing point
return false
end
end
end
-- The candidate point is valid
return true
end
-- The candidate point is outside the specified area
return false
end
-- Export the PoissonDiscSamplingModule
return PoissonDiscSamplingModule
Here’s the result of the code above, I’ve set k to 30 in the testing so it is not very precise, increasing k will make it generate points more accurately but it will also run slower.
MARTIN ROBERTS’ IMPROVED VERSION OF BRIDSON’S ALGORITHM
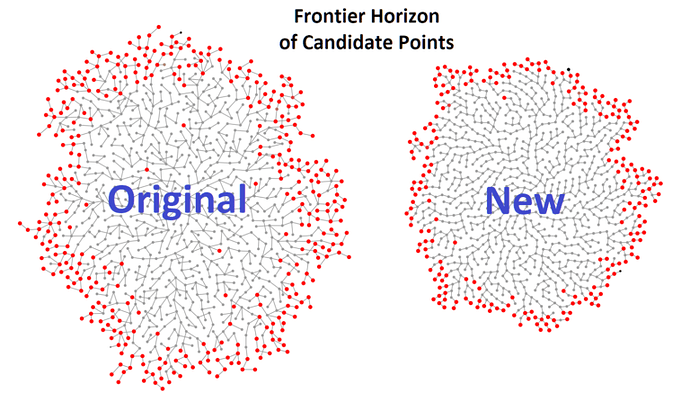
In 2019 the data scientist Martin Roberts discovered a way to make Bridson’s algorithm up to 20 times faster. Imagine you’re trying to place points in a space, but you want them to be a certain distance apart. In the original method, it’s like picking random spots inside a doughnut shape (annulus). The new way introduced by Martin Roberts is like walking around the edge of the doughnut and placing points along the way. So, instead of randomly scattering points inside the doughnut, the improved way makes a pattern by placing points around the doughnut’s edge. This makes the points closer together and looks nicer. It’s like choosing points more carefully, making the process faster and creating a better-looking result. Additionally, he adds a very small number (epsilon) to that, so they’re not exactly at the edge of the annulus to prevent errors regarding floating point numbers arithmetic.
Here’s what the code will look like once we apply those changes (I’ve commented out the section that we changed):
local PoissonDiscSamplingModule = {}
PoissonDiscSamplingModule.__index = PoissonDiscSamplingModule
function PoissonDiscSamplingModule.new(radius, area, numSamplesBeforeRejection)
local self = setmetatable({}, PoissonDiscSamplingModule)
self.radius = radius
self.area = area
self.numSamplesBeforeRejection = numSamplesBeforeRejection or 30
self.cellSize = radius / math.sqrt(2)
self.gridSizeX = math.ceil(area.X / self.cellSize)
self.gridSizeY = math.ceil(area.Y / self.cellSize)
self.grid = {}
self.points = {}
self.spawnPoints = {}
-- Initialize grid
for i = 1, self.gridSizeX do
self.grid[i] = {}
for j = 1, self.gridSizeY do
self.grid[i][j] = nil
end
end
-- Initialize spawn points
table.insert(self.spawnPoints, Vector2.new(area.X / 2, area.Y / 2))
return self
end
function PoissonDiscSamplingModule:generateNextPoint()
while #self.spawnPoints > 0 do
local spawnIndex = math.random(1, #self.spawnPoints)
local spawnCentre = self.spawnPoints[spawnIndex]
local candidateAccepted = false
local epsilon = 0.0000001
for j = 0, self.numSamplesBeforeRejection - 1 do
local angle = 2 * math.pi * (math.random() + j / self.numSamplesBeforeRejection)
local r = self.radius + epsilon
local x = spawnCentre.X + r * math.cos(angle)
local y = spawnCentre.Y + r * math.sin(angle)
if self:isValid(Vector2.new(x, y)) then
table.insert(self.points, Vector2.new(x, y))
table.insert(self.spawnPoints, Vector2.new(x, y))
local cellX = math.floor(x / self.cellSize) + 1
local cellY = math.floor(y / self.cellSize) + 1
self.grid[cellX][cellY] = #self.points
candidateAccepted = true
return Vector2.new(x, y)
end
end
if not candidateAccepted then
table.remove(self.spawnPoints, spawnIndex)
end
end
return nil
end
function PoissonDiscSamplingModule:isValid(candidate)
-- Ensure the candidate point is within the defined area
if candidate.X >= 0 and candidate.X < self.area.X and candidate.Y >= 0 and candidate.Y < self.area.Y then
-- Determine the grid cell corresponding to the candidate's position
local cellX = math.floor(candidate.X / self.cellSize) + 1
local cellY = math.floor(candidate.Y / self.cellSize) + 1
-- Precompute the square of the radius for distance comparisons
local radiusSquared = self.radius * self.radius
--[[
-- 5x5 grid, less efficient & unnecessary.
local searchStartX = math.max(1, cellX - 2)
local searchEndX = math.min(self.gridSizeX, cellX + 2)
local searchStartY = math.max(1, cellY - 2)
local searchEndY = math.min(self.gridSizeY, cellY + 2)
]]
-- Define the range of neighboring cells to check (3x3 grid around candidate)
local searchStartX = math.max(1, cellX - 1)
local searchEndX = math.min(self.gridSizeX, cellX + 1)
local searchStartY = math.max(1, cellY - 1)
local searchEndY = math.min(self.gridSizeY, cellY + 1)
-- Check each neighboring cell for potential conflicts
for x = searchStartX, searchEndX do
for y = searchStartY, searchEndY do
local pointIndex = self.grid[x][y]
if pointIndex then
local existingPoint = self.points[pointIndex]
-- Calculate squared distance
local distanceSquared = (candidate - existingPoint):Dot(candidate - existingPoint)
-- If the distance is less than the radius, the candidate is too close
if distanceSquared < radiusSquared then
return false
end
end
end
end
return true
end
return false -- out of bounds
end
-- Public function to create a PoissonDiscSamplingModule object and generate points
function PoissonDiscSamplingModule:GeneratePoints(radius, area, numSamplesBeforeRejection)
local PoissonDiscSamplingModule = PoissonDiscSamplingModule.new(radius, area, numSamplesBeforeRejection)
local generatedPoints = {}
while true do
local nextPoint = PoissonDiscSamplingModule:generateNextPoint()
if not nextPoint then
break
end
table.insert(generatedPoints, nextPoint)
end
return generatedPoints
end
return PoissonDiscSamplingModule
I am not going to show results for this, because they’re exactly the same as they were with the previous method, the difference is that this one should in theory be 20 times faster. I did not benchmark test it, though, so if anybody actually tries that let us know in the answers below whether that’s true ![]()
Instead, here’s a visualization of the difference between the two:
You can check out Martin Roberts’ original post about his algorithm here
That’s all for this tutorial, I hope you enjoyed it and it will help you somehow and let me know if you spot any mistakes, the majority of the code is tested, so it computes, but I may have made some mistakes regardless.
Note: If you’re generating a small amount of points over a relatively large area, you may not need to use any such algorithms as the chance of generating overlapping points would be small. Keep in mind that no matter how performant they are, they’re still slower than generating purely random points in a loop ![]() . It all depends specifically on what you’re attempting to make.
. It all depends specifically on what you’re attempting to make.