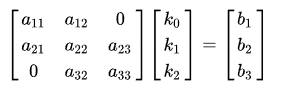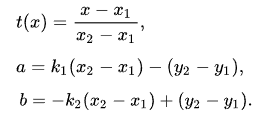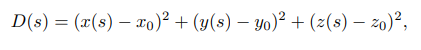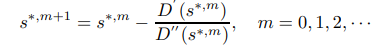First, you are going to want to come up with some list of points that represent your path. You can manually generate these points along the path or automate this. The points should be spaced close enough to each other it approximates the path relatively well. Now, we generate a set of splines which represent our entire path. You can iterate through each point (n) and select point n-1,n+1 to create a cubic spline from n-1,n,n+1. If your game isn’t too hilly, just treat the problem in 2D. Lots of algorithms exist for cubic-spline interpolation.
For 3 points, you can literally just solve for k0,k1,k2 via
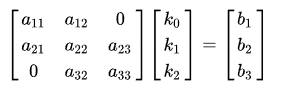

With k solved for
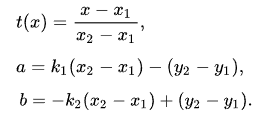
You then can obtain
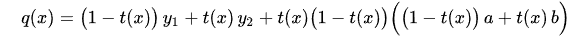
These spline segments will represent your path.
Next, we need to find the a point on the spline that is closest to a player. To do this, we can use a orthogonal projection onto the cubic spline. Academic research has been done on this topic. I will be using the paper Robust and Efficient Computation of the Closest Point on a Spline Curve (Wang, Kearney, Atikson 2002). Coincidentally, this paper is focused on roads modeled by splines as well!
First, we define L as the spline curve arc length and x(s),y(s),z(s) as the cubic spline functions.
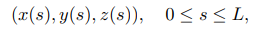
We define D(s) as the square of the distance between p0 (our player point) and the spline curve point.
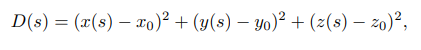
Our problem now is to calculate s* which minimizes D(s). The point on the spline curve can be referred to as p1. The vector formed by p0 and p1 must be normal to the cubic spline.
In the paper, a Newton’s method and Quadratic Minimization are used jointly to calculate a approximate solution. You can probably just use Newton’s method alone in order to achieve necessary game-performance. The formula obtained is just:
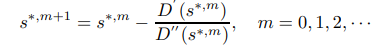
After you obtain the spline point, you can then compare value s to evaluate which player is further along the spline. This should give you a very, very accurate measure of track progression.