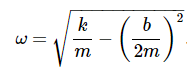I’ve tried doing this exact thing before. The lazy solution (which I did) is just to cap the maximum force the suspension could apply so that the car does not break because of the forces.
However, with low fps, the suspension will always be very different than the smooth high fps suspension when you use forces alone. If you want similar behavior you will need to find the spring height with time instead of finding the spring force with time. Unfortunately, this is quite complex to do when damping is involved as it requires calculus to integrate the forces to get a position. This is essentially what you are doing when you have high fps, but with low fps, the gaps become too large to provide values to accurately model your suspension (your suspension will overshoot).
The Equation
Luckily, damped springs are a common topic since all real-world springs have some damping to them, and there are already pre-derived equations for you to use. If you are up for the read, I found a textbook page on this that explains the equation: 15.6: Damped Oscillations - Physics LibreTexts
Essentially, they describe how to get to the equation (not really that important for implementing it), and also how to use it (more important). The two important equations for finding the height of your springs (the difference from your resting position) can be found by these two equations:
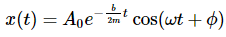
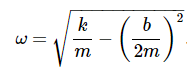
Note that you are just plugging second equation into the first equation.
To give a quick summary of the variables here: A0 is the initial height difference from your suspension’s resting position, b is the damping coefficient, k is the spring coefficient (the spring stiffness), t is time, that e is just math.exp(), m is mass, that weird sign that looks like a circle with a slash essentially just shifts the equation to a later or earlier time (for our case it can be ignored). In total, the equation graphs like this with the height difference graphed on the vertical axis and time on the horizontal axis (I already plugged in the second equation into the first equation here):
^ Damped spring!!!
Edge Cases
The textbook also explains what happens when the damping is too low or too high.
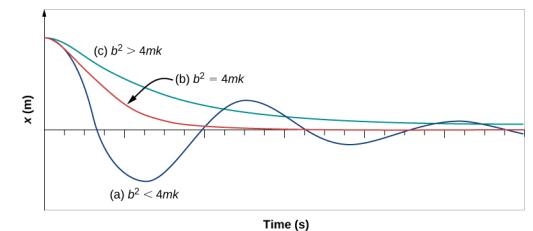
Basically if b^2 > 4mk, the damping is too high. This is the most important state to take into consideration because: 1) you probably want your suspension to reach the height you target it to and 2) when the damping is too high, the height becomes a complex number which is hard to deal with. Instead, I suggest clamping this value down to 4mk so that this does not happen.
Implementation
With all of this we can make a function that takes in time, the spring stiffness and damping coefficients, the mass of the car, and the initial height of the spring to get the current spring height.
local function getSpringHeight(deltaTime, stiffness, damping, mass, initialSpringHeight)
-- Sets stiffness back to calculable values when b^2 > 4mk
if damping ^ 2 > 4 * mass * stiffness then
stiffness = damping ^ 2 / (4 * mass)
end
local bOver2m = damping / (2 * mass)
local w = math.sqrt(stiffness / mass - bOver2m^2)
return initialSpringHeight * math.exp(-bOver2m * deltaTime) * math.cos(w * deltaTime)
end
Of course, these parameters can be minimized since most of these values do not change on every call of the function, but that is up to you for implementation. Basically what I would do is keep initialSpringHeight the same until the wheel collides with the floor again, then reset deltaTime back. The mass can be approximated by 1/4 the mass of the car. Overall, it would look something like this:
local mass = carMass / 4
local totalDeltaTime = 0
local initialHeight
local function onHitGround()
totalDeltaTime = 0
initialHeight = -- Get height from the raycast that detected ground hit
end
local function heartbeat(deltaTime)
totalDeltaTime += deltaTime
local height = getSpringHeight(totalDeltaTime, stiffness, damping, mass, initialHeight)
-- Add car reorientation code here based on spring heights
end
Overall, I did not test this, but the implementation to solve this issue is there if you decide not to go with the cheap route of clamping max force like I did. I probably will try to implement this myself in the future since this was a problem plaguing me for the longest time. Any questions are always welcome.