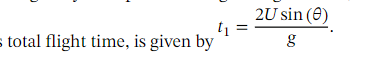Help making a system that predict where a projectile is going to land

[CoolJohnnyboy (John)]

I am looking to make a client-sided system, that will (somewhat) accurately predict where a projectile launched by a player will land, like seen below

The difference from the above and what I want is, this system will not use tools, but use turrets, the ones seen below.

I would like this system to work that it would be able to calculate where the projectile would roughly land based on the elevation and rotation of the turret. The projectile would travel in an arc/parabolic way. I am unsure of what kind of formulas I would need for this.

Where would I begin?

[81MasterGamer]

Perhaps this would be a helpful read?

Modeling a projectile's motion

This guide was originally written for scriptinghelpers. The original can be found here. As a somewhat active member of the Scripting Helpers discord one of the most common questions I see is how to have a projectile travel an arc. Most people want to know how to do this for things like basketballs or cannon balls and so forth. Since this is such a popular question I thought it would be worth writing a blog post on it and talking about a few other things we can extend from our findings. Deri…

[treebee63]

Since your projectile is a parabolic projectile affect by gravity, it should be easy to calculate EXACTLY where it’ll travel.

local function createShotPath(origin: Vector3, direction: Vector3, bulletSpeed: number)
	assert(direction.Magnitude > 0, "bullet direction cannot be 0,0,0")
	direction = direction.Unit

	local horizontal = direction * Vector3.new(1,0,1)
	local vertical = direction * Vector3.new(0,1,0)
	
	return function(t)
		-- projectile motion equation: y = y0 + v*t + 1/2 * g * t * t
		local vDelta = t * vertical * bulletSpeed - 1/2 * t * t * workspace.Gravity
		local hDelta = horizontal * t * bulletSpeed
		return origin + hDelta + vDelta
	end
end

-- suppose we spawn at bullet at 0,0,0 then fired it in the direction of 1,1,0 at speed 50
local path = createShotPath(Vector3.new(0,0,0), Vector3.new(1,1,0), 50)
print("the bullet will be at position", path(1), "1 second after launch")

If you want to draw the actual path for the projectile, EgoMoose wrote a tutorial where he uses beams to draw out the path:

Modeling a projectile's motion

[capsori (cap)]

Ok so if i were you, what i would do is
use some projectile motion physics in order to do this:
how i would use it is basically make an equation for the velocity each second,
assuming the pull force is just gravity, you can achieve something like this:

however this may be tricky because you’ll need to do this on 3 axis (x,y,z)
you give it an initial acceleration or velocity

local function primitive(t)
	local Initial = ... -- u set this to a table that contains (x,y,z) accelecrations: like { acc = {x=0, y=-workspace.Gravity, z=0}}
	local g = Initial.acc.y -- the pull force 
	local a_x = Initial.acc.x
	local a_z = Initial.acc.z
	
	return {
      a_x*t + v_x0, -- v_x0 is any value u want as initial velocity
      g*t + v_y0, -- v_y0 is any value u want as initial velocity
      a_z*t + v_z0 -- v_z0 is any value u want as initial velocity
    } -- this table now contains velocity values that we will now use to cast the projectile
end

now we’re going to apply the velocity values we got to a velocity vector
we’ll use assembly linear velocity for this

local RS = game:GetService("RunService")
local start_time = os.clock() -- this is when we start the projectile cast
local time_ = nil -- this value will keep track of the time that will update each second 
local object = ... -- the projectile object

RS.RenderStepped:Connect(function(dt: number)  -- we connect it to a render step
		time_ = os.clock() - start_time
		local velocity_equations = primitive(time_)
		
		Object.AssemblyLinearVelocity = Vector3.new(
				velocity_equations[1], -- x component
				velocity_equations[2], -- y component
				velocity_equations[3] -- z component
			)
end)

now that we have that setup, the projectile should start moving, if you want to predict its path all you have to do is calculate the trajectory time of flight, then solve to get the correspondant time value
which we will then use in the primitive function and predict where it should land

getting the trajectory length is very simple, all you have to do is:

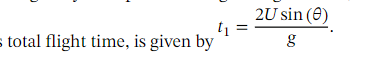
apply that equation and get the flight time,

local U = math.sqrt(velocity_equations[1]^2 + velocity_equations[2]^2 + velocity_equations[3]^2)
local two_d_norm = math.sqrt(velocity_equations[1]^2 + velocity_equations[2]^2)  -- magnitude of U in the 2d plane (x,y)
local angle =  math.acos(velocity_equations[1]/two_d_norm) -- 𝜃 we can get this on the 2d (x,y) plane no need for the z component 
local g = -workspace.Gravity

how we got the angle of the trajectory can be explained by this picture:

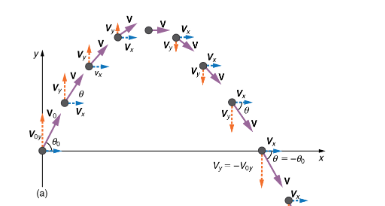
while the Velocity vector is composed of two component here Vx, Vy, finding the angle
Vx = cos(thetha) → using trignomoerty we can get the angle itself

ok, now that we have the time we just have to insert the value we found in the primitive function
then you can go from there, here’s a good resource for projectile motion
if you need more explanation, i’ll elaborate if ur going to use my method because this is still not a complete guide on proper projectile motion mechanics
https://courses.lumenlearning.com/suny-physics/chapter/3-4-projectile-motion/

hope u understand

[CoolJohnnyboy (John)]

Yeah, the drawing is what I want. I will check out that resource of yours!