How Do I Create An "Advanced Damage-Dropoff Equation" For Explosions?

[General_Ace90 (General_Ace)]

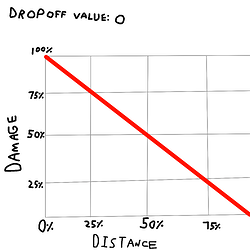
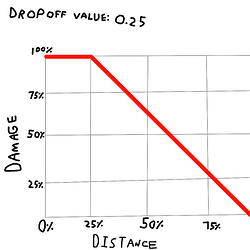
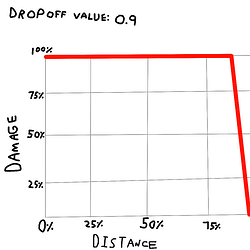
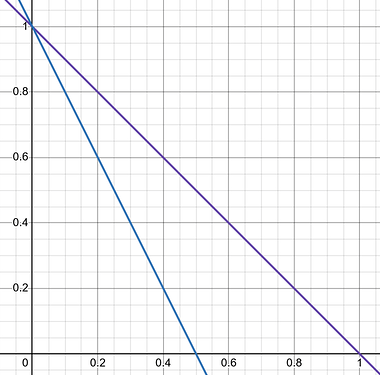
What im going for is a custom Explosion that damages both players, and destructible blocks based on distance, but only after a certain point which is controlled by a “Dropoff Value”, hence the “advanced” part. I drew some crude graphs to demonstrate what I mean below.

Distance represents the explosion’s BlastRadius with 0% being the epicenter, and 100% being on its very edge. While Damage is just the base DamageValue.

For the past while ive been using the default equation listed on the Roblox Creator Hub which is listed below:

if humanoid then
	local distanceFactor = distance / explosion.BlastRadius -- get the distance as a value between 0 and 1
	distanceFactor = 1 - distanceFactor -- flip the amount, so that lower == closer == more damage
	humanoid:TakeDamage(maxDamage * distanceFactor) -- TakeDamage to respect ForceFields
end

My version however was slightly modified to include a Dropoff Value which is listed below:

local DISTANCE_FACTOR = PART_DISTANCE / NEW_EXPLOSION.BlastRadius -- Get The Distance As A Value Between 0 And 1 For Dropoff Effects.
DISTANCE_FACTOR = 1 -DISTANCE_FACTOR -- Flip The Amount, So That Lower == Closer == More Damage.

if DISTANCE_FACTOR > DROPOFF_VALUE then -- Deal Full Damage.
	HUMANOID:TakeDamage(MAX_DAMAGE)

elseif DISTANCE_FACTOR <= DROPOFF_VALUE then -- Deal Partial Damage Based On Distance.
	HUMANOID:TakeDamage(MAX_DAMAGE * (DISTANCE_FACTOR / DROPOFF_VALUE))
end

My problem persists even when I remove the modifications and use the original equation however, so I don’t believe that to be the issue.

Basically while the equation works for the most part, i noticed while testing that sometimes the maxDamage * distanceFactor equation returns a negative number (usually near the edge of the BlastRadius) which ends up healing the player or block instead of damaging them. It seems to be mostly random, but significantly more common when maxDamage is much higher then the player or block’s MaxHealth. That’s not always the case though.

Ive played around with it and haven’t been able to solve the issue. For now I just use math.clamp() to prevent negative numbers from appearing and healing the player or block, but that still means a zero will return and players/blocks just wont take any damage when they should be.

How do I properly calculate damage dropoff like how I demonstrated in my graphs? Any help would be greatly appreciated!

[Ziffixture (Ziffix)]

You’re looking for a linear equation. The equation that describes your first graph is y = -x + 1. If you’re not familiar with this representation, its abstract form is y = mx + b. This equation describes a particular relationship between y and x, where y and x are coordinates on a Cartesian plane. m is the slope of the linear equation, which describes the rate of change of y with respect to x. b is the y-intercept, which is the value of y when x is 0. By adding a drop-off value, you change the rate of change of your linear equation. We can observe two requirements from you

1. Each linear equation must have a y-intercept of (drop-off, 1)
2. Each linear equation must have an x-intercept of (1, 0)

To make the new relationship more obvious, I’ll use your 3rd graph. Given the two points (0.5, 1) and (1, 0), the new slope of your linear equation will be equal to:

1. (0 - 1) / (1 - 0.5)
2. -1 / 0.5
3. -2

To support a drop-off of 50%, where half of the drop-off time was lost, you must now make damage drop 2x faster. We can generalize the formula for calculating the new slope as -1 / (1 - d), where d = drop-off %. Maintaining the root y-intercept of (0, 1), we get the equation:

Let’s graph this equation where d = 0, 0.5:

https://www.desmos.com/calculator/2r7rwavem5

The first graph shows the expected results, but our second graph has a deviation; we’re no longer adhering to rule #2, where the x-intercept must be (1, 0). The deviation is precisely d, so we can make the horizontal adjustment by subtracting d from x:

Here, we can see that the linear equations are now holding up as per the set rules. From this point, you need only restrict the range of the linear function to 0 <= x <= 1, so that the damage factor cannot fall below 0% or exceed 100%. However, we can simplify the function:

Here, let’s focus on the fact that d cannot equal 1, otherwise we’ll divide by 0. This isn’t desirable as d should be capable of being set to 100%. However, Luau is kind to us in that it allows zero-divisions to occur, and simply outputs positive infinity. Having already restricted the linear equation to be in the range [0, 1], this is irrelevant… at least up until the player is at a distance of 100% from the blast radius. In this scenario, the damage factor is calculated as 0/0, and will lead to the player’s health being set to NaN. This will have adverse effects. To combat this, we’ll confirm the player receives no damage when at out of range in a 100% drop-off scenario:

local function getDamageFactor(distance: number, dropOff: number): number
    if distance >= 1 and dropOff >= 1 then
        return 0
    end

    return math.clamp((1 - distance) / (1 - dropOff), 0, 1)
end

[DebtlessPenny70 (DebtPenn70)]

If you’re looking for something just like your graphs, you could use a clamped line equation.

local DISTANCE_FACTOR = PART_DISTANCE / NEW_EXPLOSION.BlastRadius

local DAMAGE_FACTOR = -(DISTANCE_FACTOR-1)/(1-DROPOFF_VALUE))
HUMANOID:TakeDamage(MAX_DAMAGE * math.clamp(DAMAGE_FACTOR,0,1))

Essentially it just makes a backwards line with some funky multiplication so that the line intersects (DROPOFF_VALUE,1) and (1,0), and then clamps it between y=0 and y=1.

I also made a Desmos graph with the same math.

[General_Ace90 (General_Ace)]

This worked beautifully! ive been testing it, and there seems to be no issues.

I was also able to significantly shorten and simplify my code.
Plus the Desmos graph was also really useful for understanding the math behind everything.
This has been really helpful, Thanks!

[Ziffixture (Ziffix)]

I’m a little hurt you accepted @DebtlessPenny70’s solution over mine, but do remember that it does not account for the edge cases I talked about. Make sure to implement the necessary code to account for them

[Ziffixture (Ziffix)]

FYI, you can simplify -(x - 1) by distributing the negative and re-arranging for: 1 - x

[imabossxd123456 (JoshLuau)]

How did bro not get the solution

[Ziffixture (Ziffix)]

I was beat by a copy-paste solution, lol