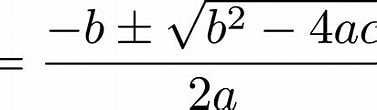How to get the landing position of a ball

Outlua · November 23, 2022, 7:49pm

Let’s say we have a 3x3x3 ball in the workspace.

Someone has kicked it, and its velocity is now Vector3.new(10, 10, 10)

But I really wonder, where is it going to land?

I need some formula to get the exact position where a ball is going to land (or bounce).

I’ve asked this before but I got some answers I can’t understand even today.

For example in volleyball, someone spikes the ball, and it lands somewhere, a position.
That’s basically want I want to accomplish (it’s most likely complex math).

If you don’t understand, we have point A, point A is like a ball, it gets kicked in the air.
The landing position is B, it’s where the ball is going to land (where it hits the ground). Now, we don’t know the ‘B’
We only know its starting position and initial velocity. I simply want to find that ‘B’

I do not want to know the velocity needed to get from point A to point B, I want to know where point B is knowing point A and the velocity.

I just can’t seem to find anything that helps me.

Please help me; Need more info? Ask me.

nicemike40 · November 23, 2022, 7:53pm

By “ground” do you mean “hits a specific Y coordinate”? Or do you need to detect collisions with anything?

astraIboy · November 23, 2022, 7:54pm

Is this ball going to have acceleration or is it going to move at a constant speed?
Is the ball going to be thrown at an angle?

Because if so youll have to incoporate these things into the equation to find the ending position

Outlua · November 23, 2022, 8:08pm

Anywhere, anywhere it lands it should count as a position. By landing, I mean hitting a BasePart. (Ground)

‘Or do you need to detect collisions with anything’ basically this

it’s like a raycast, it goes until it hits something (if the direction was enough)

Outlua · November 23, 2022, 8:13pm

Constant;

I don’t know what to say about the angle, it can be anything, but the most I’m looking for is a 90-degree turn-up or something, basically like kicking a ball high up in the air, not hitting the ground. (And then of course falling down)

Kaid3n22 · November 23, 2022, 8:21pm

If I’m understanding this correctly, you would use the velocity to get the direction and raycast to that direction.

local ball = --the ball
local ray = workspace:Raycast(ball.Position, ball.Velocity.Unit * 10) --gets any hit position within 10 units (idk if its studs)

if ray and (ray.Position or ray.Instance) then
    --found a hit position
end

You could also add a RayParams to block out anything you don’t want counted as a hit position, but this should work.

Outlua · November 23, 2022, 8:25pm

I think it works out the absolute best with bezier curves, but I don’t know how to use one.

The raycast seems to not work as well.

nicemike40 · November 23, 2022, 8:36pm

FYI Bézier curves aren’t quite right—projectiles move in parabolas

You could use the equations of projectile motion to predict your projectile’s arc, and then do a bunch of raycasts along it in small steps.

Or if you needed an exact answer I guess you could move a physical part along the path and check for IsTouchingOthers or something, binary searching to get a closer answer.

Outlua · November 23, 2022, 8:52pm

i thought of a method before this but didn’t know how to successfully do it

Basically, we make an exact copy of the ball, and just make the ball extremely fast, while also giving it a downforce.

It’s basically the same ball but sped up to get an accurate landing position, rather than waiting for the original ball to land

Doing this will make both balls hit the exact landing point

azqjanna · November 23, 2022, 9:45pm

If you only need to know if its going to hit a specific plane such as the baseplate you can use regular kinematics equations. Otherwise you can use FastCast to simulate the trajectory, which you only need to do once any time the velocity changes.

dragonvale5555 · November 23, 2022, 9:50pm

Ready for my superior knowledge of physics? (I am currently in a physics class, so hopefully I can help)

This is a situation where we would use what is called Kinematics. There are a couple main kinematics equations. I will put them here for reference

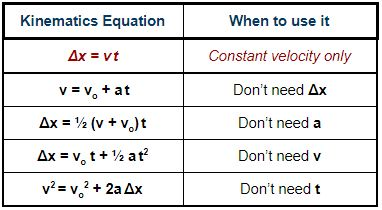
As shown by the picture, there are a few equations that would need to be used when you have specific information, but not enough. For your situation, we have the starting velocity, Vo, the acceleration, a. We also know the starting height. In order to have all of the necessary information, we need to take it in two parts. the vertical and horizontal.

In order to test it, we will assume that the initial velocity is Vector3.new(100, 250, 100), and the acceleration is going to just be Vector3.new(0, -workspace.gravity (196.2), 0). (All numbers are in studs per second)

For the vertical portion, we only need the Y component of the initial velocity. This gives us a starting velocity of 250 studs/sec and a velocity of -196.2, and a starting height of 0(above the baseplate) From there we start out with the equations.
(Visualization:)

we need to get the time that it will take for it to fall to the ground

WARNING: THIS ALL ASSUMES THAT THE LAND IS FLAT. IF IT IS NOT, MORE MATH IS INVOLVED

If that is the case, you can ping me, and I can help to flush out the kinks. (Basically you will need some raycasting to make sure that said final position is viable.)

From there we plug in the numbers to the “don’t need v(final velocity)” equation to get:
x = Vo * t + 1/2 * a * t^2
0 (starting height above baseplate) = 250 * t + 1/2 * (-196.2) * t^2
If you noticed, this is just a quadratic equation, so the quadratic formula needs to be used.
-98.1t^2 + 250t + 0 = 0

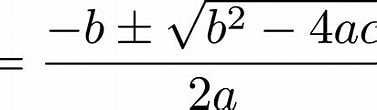
Sorry, it looks messy, idk how to format it

(250 (+-) sqrt(250^2 - 4(-98.1)(0)) / (2(-98.1)

We end up with 0, and 2.548… The 0 was already known–it started on the ground-- but now we know that it will take 2.548 seconds to hit the ground. With this, finding where it will hit is possible.
t = 2.548

Now we have the values needed: here they are:
Vo = V3(100,0,100)
V = not needed
x = ?
a = 0 (air resistance is negligable
t = 2.548

now, plug them into the “Constant Velocity Only” formula.
x = V3(100,0,100) * 2.548
x = V3(254.8, 0, 254.8)

It traveled 254.8 studs away in the x and z. That is going to be how far its position changed from before. For the actual position, you just add that to the original position.

Now for the juicy stuff… an actual script for this.

-- just add a new part into the workspace, and watch the magic happen
task.wait(3)

local function quadraticSolver(a, b, c)
	local x1 = (-b + math.sqrt((b*b) -4 * a * c)) / (2 * a)
	local x2 = (-b - math.sqrt((b*b) -4 * a * c)) / (2 * a)
	-- usually going to be x2
	return if x2 > x1 then x2 else x1
end

local function findLandingPosition(Vo: Vector3, startingPosition: Vector3)
	local acc = -workspace.Gravity
	local seconds = quadraticSolver((0.5 * acc), Vo.Y, startingPosition.Y)
	
	local horizontalVel = Vector3.new(Vo.x, 0, Vo.Z)
	local endingOffset = horizontalVel * seconds
	return startingPosition + endingOffset + Vector3.new(0, -startingPosition.Y, 0)
end


local function createPartAtLandZone(pos: Vector3)
	local part = Instance.new("Part")
	part.Size = Vector3.new(1,1,1)
	part.Shape = Enum.PartType.Ball
	part.BrickColor = BrickColor.new("Really red")
	part.Transparency = 0.5
	part.CanCollide = false
	part.Anchored = true
	part.CFrame = CFrame.new(pos)
	part.Parent = workspace	
end

local part = workspace.Part

local initialVelocity = Vector3.new(10, 100, 0)
part.AssemblyLinearVelocity = initialVelocity

createPartAtLandZone(findLandingPosition(initialVelocity, part.Position))

kaister70000 · November 23, 2022, 10:22pm

I’ve read through all the current replys, you may want to look at Fast Cast. Its kind of complicated at first but then it gets really easy and gives you all the info you need, you can have gravity, nice curves, even show the path a projectile follows. BRicey has a nice tutorial on a pistol that basically shows how to use most of fast cast if your interested.

dragonvale5555 · November 23, 2022, 10:29pm

What I wrote works perfectly and gives the projected position exactly.

thedabber777 · November 23, 2022, 10:37pm

While it most likely works properly, it is probably more efficient and easier to use Fast Cast

dragonvale5555 · November 23, 2022, 10:45pm

Fast Cast will work, but does not give you the ending position immediately as my code does. It does do raycasts though, so it does take into account characters and other obstructions, but for flat maps, my code would be more efficient and faster.

Outlua · November 26, 2022, 12:01pm

Amazing! First time in so long that someone actually shows me a source and explains.

dragonvale5555 · November 26, 2022, 9:56pm

Just be aware that the current equation assumes that you are based on a height of 0, 0 being the height of the floor. If it is anything other than 0, you will need to use the height of the floor in order to get the correct position. I modified it so that it now supports raycasting to find the real end point if there are obstructions:

-- now in a module script for accessibility and cleanliness
local maxRaycasts = 15 -- the number of raycasts to do for checking. higher = better accuracy but causes more lag in the instant that it calculates
local acc = -workspace.Gravity -- the acceleration of the world

-- just a normal function for raycasting for obstructions. Add a blacklist RaycastParams for ignore lists
local function raycast(origin, nextPoint)
	local result = workspace:Raycast(origin, (nextPoint - origin))
	return result
end

-- solve the quadratic formula for the time
local function quadraticSolver(a, b, c)
	local x1 = (-b + math.sqrt((b*b) -4 * a * c)) / (2 * a)
	local x2 = (-b - math.sqrt((b*b) -4 * a * c)) / (2 * a)
	-- usually going to be x2
	return if x2 > x1 then x2 else x1
end

-- solve for time when you put a certain height in
local function findTimeAtHeight(a, vel, h, startingH)
	local x = h - startingH
	local x1 = (math.sqrt((vel * vel) + 2 * a * x ) - vel) / a
	local x2 = -(math.sqrt((vel * vel) + 2 * a * x) + vel) / a
	return if x2 > x1 then x2 else x1
end

-- find what the height is at with input time
local function findHeightAtTime(vel, t)
	return vel.Y * t + 0.5 * acc * (t*t)
end

-- find the final position given a time
local function findPositionAtTime(vel, t, startingPos)
	local height = findHeightAtTime(vel, t)
	return startingPos + Vector3.new(vel.X * t, height, vel.Z * t)
end

-- find the final position given a height
local function findPositionAtHeight(vel, t, startingPos, height)
	return startingPos + Vector3.new(vel.X * t, height, vel.Z * t)
end

-- find the position that the part will land at based on starting velocity and position
local function findLandingPosition(Vo: Vector3, startingPosition: Vector3)
	local acc = -workspace.Gravity
	local seconds = quadraticSolver((0.5 * acc), Vo.Y, startingPosition.Y)
	local lastPosition = startingPosition

	for i = 1, maxRaycasts do
		local t = seconds * (1/maxRaycasts * i)
		local nextPosition = findPositionAtTime(Vo, t, startingPosition)

		local result = raycast(lastPosition, nextPosition)	
		if result then
			-- there was an obstruction in the way of the brick, stop the function here
			local baseHeight = result.Position.Y
			local timeAtHeight = findTimeAtHeight(acc, Vo.Y, baseHeight, startingPosition.Y)
			local offset = findPositionAtTime(Vo, timeAtHeight, startingPosition)
			return offset
		end
		lastPosition = nextPosition
	end

	local horizontalVel = Vector3.new(Vo.X, 0, Vo.Z)
	local endingOffset = horizontalVel * seconds
	return startingPosition + endingOffset + Vector3.new(0, findHeightAtTime(Vo, seconds), 0)
end

local module = {}

-- use to easily find the final pos
function module.getFinalPosition(startingVelocity: Vector3, startingPosition: Vector3)
	return findLandingPosition(startingVelocity, startingPosition)
end

return module

Does not account for the size of an object, so may give an incorrect result when next to a wall. (It will only be off in the Y axis.)

-- in a normal script
local module = require(script.positionFinder)
local pos = module.getFinalPosition(initialVelocity, initialPosition)

Outlua · November 29, 2022, 8:27am

I can add extra studs to the Y-axis for the ball, and a great one for the raycasting support too.

Outlua · November 29, 2022, 4:58pm

Do you know how to make something similar to this but instead we get the exact position of where the ball is going to stop?

Imagine this is something like 8 ball pool, when we shoot the ball, it eventually stops.

Now I need to know where it stops, instantly, as you showed me how to get the landing position instantly.

We kick the ball, we say the velocity is 25, 0, 25 (No Y needed for this)

It would be better to show the exact position, even if it hits a wall.

So it hits a wall, with a velocity of 25, 0, 25, and then gets the exact position (or something)

It should be an unlimited amount of raycasting. We need to get the position where the ball’s velocity is completely 0! It can hit as many walls as it wants to.

I tried making this myself using your quadratic solver but to no success.

Please tell me how, and show an example.

dragonvale5555 · November 29, 2022, 9:38pm

The problem with this is that the only force that is acting on it is friction, and we do not know the friction value. I will try to come up with a solution later though, but it will be harder if you just use normal roblox physics.