Is this ball going to have acceleration or is it going to move at a constant speed?
Is the ball going to be thrown at an angle?
Because if so youll have to incoporate these things into the equation to find the ending position
Anywhere, anywhere it lands it should count as a position. By landing, I mean hitting a BasePart. (Ground)
‘Or do you need to detect collisions with anything’ basically this
it’s like a raycast, it goes until it hits something (if the direction was enough)
Constant;
I don’t know what to say about the angle, it can be anything, but the most I’m looking for is a 90-degree turn-up or something, basically like kicking a ball high up in the air, not hitting the ground. (And then of course falling down)
If I’m understanding this correctly, you would use the velocity to get the direction and raycast to that direction.
local ball = --the ball
local ray = workspace:Raycast(ball.Position, ball.Velocity.Unit * 10) --gets any hit position within 10 units (idk if its studs)
if ray and (ray.Position or ray.Instance) then
--found a hit position
end
You could also add a RayParams to block out anything you don’t want counted as a hit position, but this should work.
I think it works out the absolute best with bezier curves, but I don’t know how to use one.
The raycast seems to not work as well.
FYI Bézier curves aren’t quite right—projectiles move in parabolas
You could use the equations of projectile motion to predict your projectile’s arc, and then do a bunch of raycasts along it in small steps.
Or if you needed an exact answer I guess you could move a physical part along the path and check for IsTouchingOthers or something, binary searching to get a closer answer.
i thought of a method before this but didn’t know how to successfully do it
Basically, we make an exact copy of the ball, and just make the ball extremely fast, while also giving it a downforce.
It’s basically the same ball but sped up to get an accurate landing position, rather than waiting for the original ball to land
Doing this will make both balls hit the exact landing point
If you only need to know if its going to hit a specific plane such as the baseplate you can use regular kinematics equations. Otherwise you can use FastCast to simulate the trajectory, which you only need to do once any time the velocity changes.
Ready for my superior knowledge of physics? (I am currently in a physics class, so hopefully I can help)
This is a situation where we would use what is called Kinematics. There are a couple main kinematics equations. I will put them here for reference
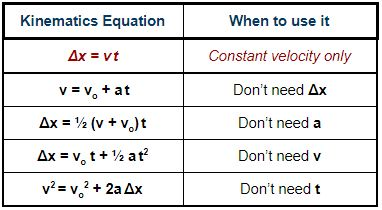
As shown by the picture, there are a few equations that would need to be used when you have specific information, but not enough. For your situation, we have the starting velocity, Vo, the acceleration, a. We also know the starting height. In order to have all of the necessary information, we need to take it in two parts. the vertical and horizontal.
In order to test it, we will assume that the initial velocity is Vector3.new(100, 250, 100), and the acceleration is going to just be Vector3.new(0, -workspace.gravity (196.2), 0). (All numbers are in studs per second)
For the vertical portion, we only need the Y component of the initial velocity. This gives us a starting velocity of 250 studs/sec and a velocity of -196.2, and a starting height of 0(above the baseplate) From there we start out with the equations.
(Visualization:)
we need to get the time that it will take for it to fall to the ground
WARNING: THIS ALL ASSUMES THAT THE LAND IS FLAT. IF IT IS NOT, MORE MATH IS INVOLVED
If that is the case, you can ping me, and I can help to flush out the kinks. (Basically you will need some raycasting to make sure that said final position is viable.)
From there we plug in the numbers to the “don’t need v(final velocity)” equation to get:
x = Vo * t + 1/2 * a * t^2
0 (starting height above baseplate) = 250 * t + 1/2 * (-196.2) * t^2
If you noticed, this is just a quadratic equation, so the quadratic formula needs to be used.
-98.1t^2 + 250t + 0 = 0
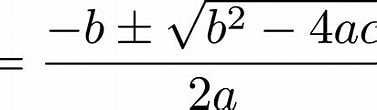
Sorry, it looks messy, idk how to format it
(250 (+-) sqrt(250^2 - 4(-98.1)(0)) / (2(-98.1)
We end up with 0, and 2.548… The 0 was already known–it started on the ground-- but now we know that it will take 2.548 seconds to hit the ground. With this, finding where it will hit is possible.
t = 2.548
Now we have the values needed: here they are:
Vo = V3(100,0,100)
V = not needed
x = ?
a = 0 (air resistance is negligable
t = 2.548
now, plug them into the “Constant Velocity Only” formula.
x = V3(100,0,100) * 2.548
x = V3(254.8, 0, 254.8)
It traveled 254.8 studs away in the x and z. That is going to be how far its position changed from before. For the actual position, you just add that to the original position.
Now for the juicy stuff… an actual script for this.
-- just add a new part into the workspace, and watch the magic happen
task.wait(3)
local function quadraticSolver(a, b, c)
local x1 = (-b + math.sqrt((b*b) -4 * a * c)) / (2 * a)
local x2 = (-b - math.sqrt((b*b) -4 * a * c)) / (2 * a)
-- usually going to be x2
return if x2 > x1 then x2 else x1
end
local function findLandingPosition(Vo: Vector3, startingPosition: Vector3)
local acc = -workspace.Gravity
local seconds = quadraticSolver((0.5 * acc), Vo.Y, startingPosition.Y)
local horizontalVel = Vector3.new(Vo.x, 0, Vo.Z)
local endingOffset = horizontalVel * seconds
return startingPosition + endingOffset + Vector3.new(0, -startingPosition.Y, 0)
end
local function createPartAtLandZone(pos: Vector3)
local part = Instance.new("Part")
part.Size = Vector3.new(1,1,1)
part.Shape = Enum.PartType.Ball
part.BrickColor = BrickColor.new("Really red")
part.Transparency = 0.5
part.CanCollide = false
part.Anchored = true
part.CFrame = CFrame.new(pos)
part.Parent = workspace
end
local part = workspace.Part
local initialVelocity = Vector3.new(10, 100, 0)
part.AssemblyLinearVelocity = initialVelocity
createPartAtLandZone(findLandingPosition(initialVelocity, part.Position))
4 Likes
I’ve read through all the current replys, you may want to look at Fast Cast. Its kind of complicated at first but then it gets really easy and gives you all the info you need, you can have gravity, nice curves, even show the path a projectile follows. BRicey has a nice tutorial on a pistol that basically shows how to use most of fast cast if your interested.
What I wrote works perfectly and gives the projected position exactly.
While it most likely works properly, it is probably more efficient and easier to use Fast Cast
Fast Cast will work, but does not give you the ending position immediately as my code does. It does do raycasts though, so it does take into account characters and other obstructions, but for flat maps, my code would be more efficient and faster.
Amazing! First time in so long that someone actually shows me a source and explains.
Just be aware that the current equation assumes that you are based on a height of 0, 0 being the height of the floor. If it is anything other than 0, you will need to use the height of the floor in order to get the correct position. I modified it so that it now supports raycasting to find the real end point if there are obstructions:
-- now in a module script for accessibility and cleanliness
local maxRaycasts = 15 -- the number of raycasts to do for checking. higher = better accuracy but causes more lag in the instant that it calculates
local acc = -workspace.Gravity -- the acceleration of the world
-- just a normal function for raycasting for obstructions. Add a blacklist RaycastParams for ignore lists
local function raycast(origin, nextPoint)
local result = workspace:Raycast(origin, (nextPoint - origin))
return result
end
-- solve the quadratic formula for the time
local function quadraticSolver(a, b, c)
local x1 = (-b + math.sqrt((b*b) -4 * a * c)) / (2 * a)
local x2 = (-b - math.sqrt((b*b) -4 * a * c)) / (2 * a)
-- usually going to be x2
return if x2 > x1 then x2 else x1
end
-- solve for time when you put a certain height in
local function findTimeAtHeight(a, vel, h, startingH)
local x = h - startingH
local x1 = (math.sqrt((vel * vel) + 2 * a * x ) - vel) / a
local x2 = -(math.sqrt((vel * vel) + 2 * a * x) + vel) / a
return if x2 > x1 then x2 else x1
end
-- find what the height is at with input time
local function findHeightAtTime(vel, t)
return vel.Y * t + 0.5 * acc * (t*t)
end
-- find the final position given a time
local function findPositionAtTime(vel, t, startingPos)
local height = findHeightAtTime(vel, t)
return startingPos + Vector3.new(vel.X * t, height, vel.Z * t)
end
-- find the final position given a height
local function findPositionAtHeight(vel, t, startingPos, height)
return startingPos + Vector3.new(vel.X * t, height, vel.Z * t)
end
-- find the position that the part will land at based on starting velocity and position
local function findLandingPosition(Vo: Vector3, startingPosition: Vector3)
local acc = -workspace.Gravity
local seconds = quadraticSolver((0.5 * acc), Vo.Y, startingPosition.Y)
local lastPosition = startingPosition
for i = 1, maxRaycasts do
local t = seconds * (1/maxRaycasts * i)
local nextPosition = findPositionAtTime(Vo, t, startingPosition)
local result = raycast(lastPosition, nextPosition)
if result then
-- there was an obstruction in the way of the brick, stop the function here
local baseHeight = result.Position.Y
local timeAtHeight = findTimeAtHeight(acc, Vo.Y, baseHeight, startingPosition.Y)
local offset = findPositionAtTime(Vo, timeAtHeight, startingPosition)
return offset
end
lastPosition = nextPosition
end
local horizontalVel = Vector3.new(Vo.X, 0, Vo.Z)
local endingOffset = horizontalVel * seconds
return startingPosition + endingOffset + Vector3.new(0, findHeightAtTime(Vo, seconds), 0)
end
local module = {}
-- use to easily find the final pos
function module.getFinalPosition(startingVelocity: Vector3, startingPosition: Vector3)
return findLandingPosition(startingVelocity, startingPosition)
end
return module
Does not account for the size of an object, so may give an incorrect result when next to a wall. (It will only be off in the Y axis.)
-- in a normal script
local module = require(script.positionFinder)
local pos = module.getFinalPosition(initialVelocity, initialPosition)
5 Likes
I can add extra studs to the Y-axis for the ball, and a great one for the raycasting support too.
Do you know how to make something similar to this but instead we get the exact position of where the ball is going to stop?
Imagine this is something like 8 ball pool, when we shoot the ball, it eventually stops.
Now I need to know where it stops, instantly, as you showed me how to get the landing position instantly.
We kick the ball, we say the velocity is 25, 0, 25 (No Y needed for this)
It would be better to show the exact position, even if it hits a wall.
So it hits a wall, with a velocity of 25, 0, 25, and then gets the exact position (or something)
It should be an unlimited amount of raycasting. We need to get the position where the ball’s velocity is completely 0! It can hit as many walls as it wants to.
I tried making this myself using your quadratic solver but to no success.
Please tell me how, and show an example.
The problem with this is that the only force that is acting on it is friction, and we do not know the friction value. I will try to come up with a solution later though, but it will be harder if you just use normal roblox physics.
1 Like
Ok, so unfortunately the physics behind a ball rolling on the ground are very complicated than I thought and not something that I know at this point in time. I don’t think that I will be able to come up with a way to find the position for when it stops. Sorry. Maybe sometime in the future. I’ll DM if I ever figure it out.
1 Like
This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.