Optimizing our A*
In the previous part, we delved into the basics of the A* algorithm, an essential tool in pathfinding and graph traversal. This section will be dedicated to optimizing our A* algorithm for greatly improved performance. In addition to this, we’ll also explore some intriguing variants of the algorithm, broadening the versatility and reliability of our algorithm at our disposal. But thats for the next part!
DISCLAIMER
If you’re looking for a pathfinding solution to fit your needs, I highly recommend researching about other variants of A*, such as D*; which performs better than A* in a more dynamic environment
Looking back at our implementation
local SIZE = 5
local DIRECTIONS = {
Vector3.xAxis;
Vector3.zAxis;
Vector3.xAxis * -1;
Vector3.zAxis * -1;
Vector3.zAxis + Vector3.xAxis;
Vector3.xAxis * -1 + Vector3.zAxis;
Vector3.xAxis + Vector3.zAxis * -1;
}
for i, dir in DIRECTIONS do
DIRECTIONS[i] = dir * SIZE -- scale the directions with the grid size
end
local function RoundToNearest(v)
return Vector3.new(
math.round(v.X / SIZE) * SIZE,
math.round(v.Y / SIZE) * SIZE,
math.round(v.Z / SIZE) * SIZE
)
end
local function ConstructNode(a: Vector3, b: Vector3, gc)
local function HeuristicFunction()
return math.abs(a.X - b.X) + math.abs(a.Y - b.Y) + math.abs(a.Z - b.Z)
end
local hc = HeuristicFunction()
return {
Position = a;
Costs = {
G = gc;
H = hc;
F = gc + hc;
};
}
end
local function NodeIsTraversable(point: Vector3)
local collisions = workspace:GetPartBoundsInBox(CFrame.new(point), Vector3.new(SIZE, 0, SIZE))
if collisions[1] then
return false
end
return true
end
function FindPath(start: Vector3, target: Vector3)
local OpenSet = { ConstructNode(start, target, 0) }
local ClosedSet = {}
local Parents = {}
start = RoundToNearest(start)
target = RoundToNearest(target)
local function FindNodeInOpenSet(point: Vector3)
for _, node in OpenSet do
if node.Position == point then
return node
end
end
end
local function RetracePath()
local Path = {}
local CurrentNode = target
while CurrentNode ~= start do
table.insert(Path, 1, CurrentNode)
CurrentNode = Parents[CurrentNode]
end
return Path
end
while OpenSet[1] do -- checks if theres any nodes left to be evaluated
table.sort(OpenSet, function(a, b)
return a.Costs.F <= b.Costs.F and a.Costs.H < b.Costs.H
end)
local Node = table.remove(OpenSet, 1)
if Node.Position == target then -- checks if node is the target
return RetracePath()
end
ClosedSet[Node.Position] = true
for _, direction in DIRECTIONS do
local Neighbor = Node.Position + direction
local IsTraversable = NodeIsTraversable(Neighbor)
if not IsTraversable or ClosedSet[Neighbor] then
continue
end
local Distance = (Node.Position - Neighbor).Magnitude -- basically the G cost
local CostToNeighbor = Node.Costs.G + Distance
local NeighborNode = FindNodeInOpenSet(Neighbor)
local NeighborGCost = NeighborNode and NeighborNode.Costs.G or 0 -- if neighbour node exists, then get the g cost, else its 0
if CostToNeighbor < NeighborGCost or not NeighborNode then
table.insert(OpenSet, ConstructNode(Neighbor, target, CostToNeighbor))
Parents[Neighbor] = Node.Position
end
end
end
end
The issue with our current implementation is the (super slow) sorting function and the (even slower) node lookup function.
To optimize our implementation, we will transform the OpenSet from an array into a dictionary or table. In this revised structure, the key will be set to the node’s position, and the value will be the node object itself. This change will allow us to perform lookups more efficiently, as we can directly access any node in the OpenSet using its position, thus eliminating the need for slow, iterative search processes.
Position-node lookup optimization
function FindPath(start: Vector3, target: Vector3)
local OpenSet = { [start] = ConstructNode(start, target, 0) }
local ClosedSet = {}
local Parents = {}
start = RoundToNearest(start)
target = RoundToNearest(target)
local function RetracePath()
-- ...
end
while next(OpenSet) do
local Node = OpenSet[1]
for _, v in OpenSet do -- we have to do a for loop since its a table now
if v.Costs.F <= Node.Costs.F and v.Costs.H < Node.Costs.H then
Node = v
end
end
if Node.Position == target then -- checks if node is the target
return RetracePath()
end
ClosedSet[Node.Position] = true
for _, direction in DIRECTIONS do
local Neighbor = Node.Position + direction
local IsTraversable = NodeIsTraversable(Neighbor)
if not IsTraversable or ClosedSet[Neighbor] then
return
end
local Distance = (Node.Position - Neighbor).Magnitude -- basically the G cost
local CostToNeighbor = Node.Costs.G + Distance
local NeighborNode = OpenSet[Neighbor]
local NeighborGCost = NeighborNode and NeighborNode.Costs.G or 0 -- if neighbour node exists, then get the g cost, else its 0
if CostToNeighbor < NeighborGCost or not NeighborNode then
OpenSet[target] = ConstructNode(Neighbor, target, CostToNeighbor)
Parents[Neighbor] = Node.Position
end
end
end
end
Alright, here’s the scoop! We’ve made a few tweaks to our A* implementation. The big game changer here is that we’ve turned our OpenSet from an array into a dictionary or table. With this switcheroo, we now use the node’s position as the key and the node object as the value. This neat little trick gives us ![]() access to any node in the
access to any node in the OpenSet using its position. Say goodbye to those slow, draggy search processes! Now, isn’t that a breath of fresh air?
But hang on, we still have a somewhat pricey procedure to go through - the sorting! So, how can we achieve the smallest F and H costs, while still keeping things speedy? For that, let’s dig into the world of sorting algorithms, shall we?
Sorting Algorithms for A*
When it comes to selecting the right sorting algorithm for our A* implementation, we’re really looking for an algorithm that can efficiently handle the task of always finding and extracting the node with the smallest F cost, and in the case of a tie, the smallest H cost.
There are numerous sorting algorithms out there, such as Quick Sort, Merge Sort, Insertion Sort, and Heap Sort. While Quick Sort and Merge Sort are efficient for large data sets, they aren’t the best fit here because they don’t efficiently handle dynamic data. Insertion Sort, on the other hand, performs well with small data sets or nearly sorted data, but less so for larger, unsorted data sets.
Heap Sort, however, stands out as an optimal choice for our needs.
Heap Sort
Heap Sort is an in-place sorting algorithm that builds a binary heap and uses it to sort the elements. The beauty of Heap Sort is that it maintains the heap property - that is, the parent node is always either greater than or equal to (in a max heap) or less than or equal to (in a min heap) its children. This property ensures that the smallest (or largest) element is always at the root of the heap.
For our A* implementation, we can use a min heap to keep track of our nodes. After each insertion or deletion, we’ll ‘heapify’ to ensure the node with the smallest F cost (and smallest H cost in case of a tie) is always at the root. When we need the node with the smallest cost, we simply extract the root node.
To make our code easier to read and navigate through, we will create a Heap class
local Heap = {}
function Heap.new<T>() -- Just some typechecking stuff we'll be using later on
-- Our heap private virables
local Items = {} :: {[number]: {HeapIndex: number} & T} -- The items in our heap tree (in this case, our nodes)
local CurrentItemCount = 0 -- The number of items currently in our tree
local Object = {} -- The class' instantiated object
return Object
end
return Heap
Just like all sorting algorithms, let’s treat ourselves to a little Swap function, shall we?
local Heap = {}
function Heap.new<T>() -- Just some typechecking stuff we'll be using later on
-- Our heap private virables
local Items = {} :: {[number]: {HeapIndex: number} & T} -- The items in our heap tree (in this case, our nodes)
local CurrentItemCount = 0 -- The number of items currently in our tree
local function Swap(a, b)
Items[a.HeapIndex], Items[b.HeapIndex] = b, a
local itemAIndex = a.HeapIndex
a.HeapIndex = b.HeapIndex
b.HeapIndex = itemAIndex
end
local Object = {} -- The class' instantiated object
return Object
end
return Heap
Sorting up in a heap tree is a method of arranging data in a tree-like structure, called a binary heap, where each node has at most two children and the key of each node is greater than or equal to (in a max heap) or less than or equal to (in a min heap) the keys of its children. This allows for efficient insertion, deletion, and search operations, and is commonly used in computer science for tasks such as implementing priority queues and sorting algorithms.
local Heap = {}
function Heap.new<T>() -- Just some typechecking stuff we'll be using later on
-- Our heap private virables
type Item = {HeapIndex: number} & T
local Items = {} :: {[number]: Item} -- The items in our heap tree (in this case, our nodes)
local CurrentItemCount = 0 -- The number of items currently in our tree
local function Swap(a: Item, b: Item)
Items[a.HeapIndex], Items[b.HeapIndex] = b, a
local itemAIndex = a.HeapIndex
a.HeapIndex = b.HeapIndex
b.HeapIndex = itemAIndex
end
local function SortUp(item: Item)
local parentIndex = (item.HeapIndex-1)/2
while true do
local parentItem = Items[parentIndex]
-- Check if the parent item exists and if the item is greater than the parent
if parentItem and item - parentItem > 0 then
-- If so, swap the item with the parent item
Swap(item, parentItem)
else
-- Otherwise, the item is in the correct position, so break out of the loop
break
end
parentIndex = (item.HeapIndex-1)/2
end
end
local Object = {} -- The class' instantiated object
function Object:Add(item: Item)
item.HeapIndex = CurrentItemCount
Items[CurrentItemCount] = item
SortUp(item) -- Sort up since our heap item is at the bottom
CurrentItemCount += 1
end
function Object:Contains(item: Item)
return Items[item.HeapIndex] == item
end
function Object:Count() -- Just a simple getter
return CurrentItemCount
end
return Object
end
return Heap
Oh wait, did you notice that?
if parentItem and item - parentItem > 0 then
We are substracting a table! Wouldn’t it just error?
And that I answer; yes. But with the help of ![]() metatables
metatables ![]() , we can subtract a table with another table. Heck, you can even check if the node is equal to another node in terms of its position!
, we can subtract a table with another table. Heck, you can even check if the node is equal to another node in terms of its position!
To implement our metatables, we can do the following to our Node constructor function
local function ConstructNode(worldPos: Vector3, target: Vector3)
local Object = setmetatable({
Traversable = false;
Position = worldPos;
Costs = setmetatable({
G = 0;
H = 0;
}, {
__index = function(t, k)
if k == 'F' then
return rawget(t, 'H') + rawget(t, 'G') -- F is the sum of H and G
end
return rawget(t, k)
end,
});
HeapIndex = 0; -- For our new heap
Parent = nil; -- No more storing Parents table
}, {
__sub = function(a, b)
local compare = a.Costs.F - b.Costs.F -- Substract a's F and b's F
if compare == 0 then -- If the F costs are equal, compare the H cost instead
compare = a.Costs.H - b.Costs.H
end
return -compare -- Return the negated comparison
end,
__eq = function(a, b)
return a.Position == b.Position
end,
})
Object.Costs.G = (worldPos - target).Magnitude
Object.Costs.H = HeuristicFunction and HeuristicFunction(worldPos, target) or 0 -- Heuristic is 0 if no function is set
Object.Traversable = NodeIsTraversable(worldPos)
return Object
end
But now we need a way to get the root node (which is the lowest in cost). And to do that we need… you guessed it - a sort down function!
local Heap = {}
function Heap.new<T>() -- Just some typechecking stuff we'll be using later on
-- Our heap private virables
type Item = {HeapIndex: number} & T
local Items = {} :: {[number]: Item} -- The items in our heap tree (in this case, our nodes)
local CurrentItemCount = 0 -- The number of items currently in our tree
local function Swap(a: Item, b: Item)
Items[a.HeapIndex], Items[b.HeapIndex] = b, a
local itemAIndex = a.HeapIndex
a.HeapIndex = b.HeapIndex
b.HeapIndex = itemAIndex
end
local function SortUp(item: Item)
local parentIndex = (item.HeapIndex-1)/2
while true do
local parentItem = Items[parentIndex]
-- Check if the parent item exists and if the item is greater than the parent
if parentItem and item - parentItem > 0 then
-- If so, swap the item with the parent item
Swap(item, parentItem)
else
-- Otherwise, the item is in the correct position, so break out of the loop
break
end
parentIndex = (item.HeapIndex-1)/2
end
end
local function SortDown(item: Item)
while true do
local childLeftIndex = item.HeapIndex * 2 + 1
local childRightIndex = item.HeapIndex * 2 + 2
local swapIndex = 0
-- Check if the left child exists
if childLeftIndex < CurrentItemCount then
swapIndex = childLeftIndex
-- If the right child has a higher priority, set the swap index to the right child index
if childRightIndex < CurrentItemCount then
-- If so, compare the priorities of the left and right children
if Items[childLeftIndex] - Items[childRightIndex] < 0 then
-- If the right child has a higher priority, set the swap index to the right child index
swapIndex = childRightIndex
end
end
-- Compare the priority of the item with the priority of the child at the swap index
if item-Items[swapIndex] < 0 then
-- If the child has a higher priority, swap the item with the child
Swap(item, Items[swapIndex])
else
-- Otherwise, the item is in the correct position, so break out of the loop
return
end
else
-- If the left child does not exist, the item is at the bottom of the heap and in the correct position
return
end
end
end
local Object = {} -- The class' instantiated object
function Object:RemoveFirst() : Item
local firstItem = Items[0] -- Get the root node
CurrentItemCount -= 1 -- Decrease the items count
Items[0] = Items[CurrentItemCount] -- Set the root node to lowest item
Items[0].HeapIndex = 0
SortDown(Items[0]) -- Sort down since the lowest item is at the root node
return firstItem
end
function Object:Add(item: Item)
item.HeapIndex = CurrentItemCount
Items[CurrentItemCount] = item
SortUp(item) -- Sort up since our heap item is at the bottom
CurrentItemCount += 1
end
function Object:Contains(item: T)
return Items[item.HeapIndex] == item
end
function Object:Count() -- Just a simple getter
return CurrentItemCount
end
return Object
end
return Heap
And now for the FindPath function, we can simply do:
local function FindPath(start: Vector3, target: Vector3)
start = RoundToNearest(start)
target = RoundToNearest(target)
local StartNode = ConstructNode(start, target)
local TargetNode = ConstructNode(target, target)
-- Safety precaution checks so we don't waste time computing the path
assert(StartNode.Traversable, 'Starting Node is intraversable, thus path is intraversable')
assert(TargetNode.Traversable, 'Target Node is intraversable, thus path is intraversable')
local Grid = {[start] = StartNode, [target] = TargetNode}
local OpenSet = Heap.new() :: Heap.Heap<typeof(ConstructNode(Vector3, Vector3))>
local ClosedSet = {}
OpenSet:Add(StartNode)
while OpenSet:Count() > 0 do
local CurrentNode = OpenSet:RemoveFirst()
ClosedSet[CurrentNode.Position] = true
if CurrentNode == TargetNode then
-- we'll come back to this later
end
for _, direction in DIRECTIONS do
local NeighborPos = CurrentNode.Position + direction
-- If neighbor already evaluated/not traversable, skip
if ClosedSet[NeighborPos] or not NodeIsTraversable(NeighborPos) then
continue
end
-- Get neighbor node
local NeighborNode = Grid[NeighborPos] or ConstructNode(NeighborPos, target)
Grid[NeighborPos] = NeighborNode
-- Get new G cost to the neighbor
local CostToNeighbor = CurrentNode.Costs.G + (CurrentNode.Position - NeighborPos).Magnitude
-- If cost turns out to be better or not in openset
if CostToNeighbor < NeighborNode.Costs.G or not OpenSet:Contains(NeighborNode) then
NeighborNode.Costs.G = CostToNeighbor
NeighborNode.Costs.H = (NeighborPos, target).Magnitude
NeighborNode.Parent = CurrentNode
if not OpenSet:Contains(NeighborNode) then -- If it doesn't have the neighbor node yet, add the node
OpenSet:Add(NeighborNode)
end
end
end
end
end
Now, since we’re using a new member of the node to get the parent, we need to revise our retrace path function:
local function RetracePath()
local Path = {}
local CurrentPathNode = TargetNode
while CurrentPathNode ~= StartNode do
table.insert(Path, 1, CurrentPathNode)
CurrentPathNode = CurrentPathNode.Parent
end
return Path
end
if CurrentNode == TargetNode then
return RetracePath()
end
Heuristics
Heuristic is what makes your algorithm performs better. Different heuristics have different environment usages. For example, take the manhattan distance heuristic:
local function HeuristicFunction(a: Vector3, b: Vector3): number
local dx = math.abs(a.x - b.x)
local dy = math.abs(a.y - b.y)
local dz = math.abs(a.z - b.z)
return dx + dy + dz
end
The Manhattan distance heuristic function calculates the distance between two points based on the sum of the (absolute) differences of their coordinates. This heuristic is most appropriate for use in pathfinding algorithms when the path between the start and goal nodes is expected to be primarily composed of horizontal and vertical movements
local function HeuristicFunction(a: Vector3, b: Vector3): number
local dx = a.x - b.x
local dy = a.y - b.y
local dz = a.z - b.z
return math.sqrt(dx * dx + dy * dy + dz * dz)
end
The Euclidean distance heuristic function calculates the straight-line distance between two points in 3D space. This heuristic is most appropriate for use in pathfinding algorithms when the path between the start and goal nodes is expected to be relatively unobstructed
local D = math.sqrt(2) -- A constant
local function HeuristicFunction(a: Vector3, b: Vector3): number
local D2 = 1
local dx = math.abs(a.X - b.X)
local dy = math.abs(a.Y - b.Y)
local dz = math.abs(a.Z - b.Z)
return D * math.min(dx, dy, dz) + (D2 - D) * math.max(0, dx + dy + dz - 2 * math.min(dx, dy, dz))
end
The Octile distance heuristic function calculates the distance between two points based on the maximum of the (absolute differences of their coordinates, multiplied by a constant factor sqrt(2)-1 and added to the minimum distance in one of the axis multiplied by the square root of 2. This heuristic is most appropriate for use in pathfinding algorithms when the path between the start and goal nodes is expected to be composed of diagonal movements
TL;DR
→ Diagonal = Octile
→ Horizontal & vertical = Euclidean
→ Unobstructed/Less obstacles = Manhattan
Keep in mind that the Octile Heuristic is the most expensive one out of the 2 other options, which Octile uses min, max, and abs with greater frequency than that of the other heuristics.
Some heuristics handles open-space environment better, but handles closed-space environment worse (in terms of computation time); and vice-versa
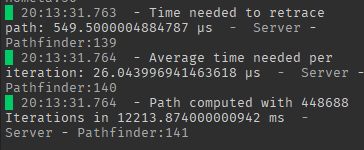
As a quick boost in performance (in terms of speed); you can put --!native and --!optimize 2 on all of the related scripts and modules. In the next part, we will be exploring other variants of the A* algorithm, such that handles dynamic environments even better.
Hope you enjoyed this tutorial. Sorry for the long wait, I’m kind of squashed between projects that I have dedicated on. As always, If theres any mistakes in this, please correct me. And if you have any questions or concerns regarding A*, ask away!
- yes!!!
- no!!! i want the most optimal global optima fast execution time low memory overhead
0 voters