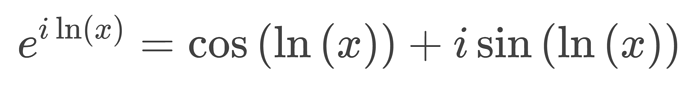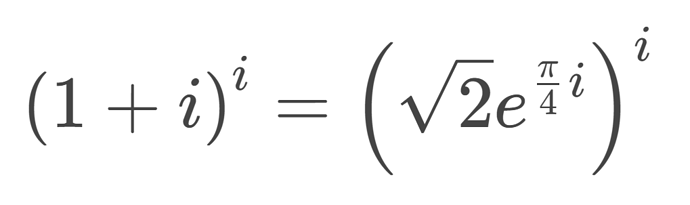Introducing MathAddons!

[CoderHusk]

Thanks, the int check was helpful for debugging

[Squiegy (Squared)]

Four New Functions! (& Minor Code Optimizations)

1) Scientific Format

Purpose
Returns true/false depending on whether an integer is prime
Parameters
1 - number
2 - any value that toggles e or exponential notation
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.science(3189263)) -- since there is no 2nd parameter, itll return 3.189263 * 10^6
print(module.science(3189263),'a') -- since the 2nd parameter isnt nil anymore it returns  3.189263e6

Real Situation
Turn big numbers into readable ones

local module = require(game.ReplicatedStorage.MathAddons)
local bigNum = 85123651283
local formatted = module.science(85123651283)

You can undo this function by using the module.rscience() function

local module = require(game.ReplicatedStorage.MathAddons)
local bigNum = 85123651283
local formatted = module.science(85123651283)
print(module.rscience(formatted)) -- returns 85123651283

II) Roman Numerals

Purpose
Convert integers into roman numerals
Parameters
1 - integer
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.roman(5)) -- V
print(module.roman(12)) -- XII
print(module.roman(9)) -- IIV

Real Situation
You’re making a rank system every few levels they advance to a new rank, in those levels they progress in rank I, rank II, rank III, rank IV…

local module = require(game.ReplicatedStorage.MathAddons)
local rankTable = {'Noob','Okay', 'Good', 'Great', 'Pro', 'Advanced', 'Best', 'God Level'}
local level = 41
local levelsPerRank = 6
player.stats.Rank.Value = rankTable[math.floor(level/levelsPerRank)].. module.roman(level%levelsPerRank)
-- since 41/6 is 6 rounded down, the 6th index in the table is advanced, and 5 is left over, so the rank would be "Advanced V"

3) KMBT Format

Purpose
convert numbers into kmbt
Parameters
1 - number at least 1000
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.kmbt(123456789)) -- 123.45M 
print(module.kmbt(1234)) -- 1.23K
print(a.kmbt(1234567890123456789012345678901234567890)) --1.23Ddc

Real Situation
You have a currency system with large values

local module = require(game.ReplicatedStorage.MathAddons)
currency:GetPropertyChangedSignal('Value'):Connect(function()
script.Parent.Text = module.kmbt(currency.Value)
end)

4) Equation Solver

Purpose
Solve a math equation in the form of mx+b=y (can be mx=y or x+b=y or even x=y)
Parameters
1 - string
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.equation('2x+3=8')) -- subtract 3 from both sides and divide both sides by 2 (8-3=5, 5/2 = 2.5), x = 2.5

Real Situation
I think this was cool

This module will get updated every time i come up with a useful tool to add!
Get the updated version here
MathAddons

[Velliaan (Milenda Foranzi)]

If a number goes into the negatives when using math.kmbt(myNumber) it won’t format it even if its in the negative by millions

[Squiegy (Squared)]

My bad, I overlooked the issue with negative inputs, the kmbt format (comma format, and scientific notation) now work properly with negatives

[Squiegy (Squared)]

Changes

3 New, and completely useless functions

15) Integration

Purpose
Get the integral of a given function with lower and upper bounds
Parameters
1 - Precision [There aren’t limits in programming, how accurate do you want it to be?] (Number)
2 - Lower Bound [Whats the lower bound of the integral?] (Number)
3 - Upper Bound [What’s the upper bound of the integral?] (Number)
4 - Integrand [What function are you integrating?] (Function)
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(integral(.01,0,10,function(x)
	return x^2
end)) -- This is approximately 1000/3 [333.83349999999007]

This function is equivalent to:

16) Derivatives

Purpose
Find the rate of change at a certain input of a function
Parameters
1 - Precision [There aren’t limits in programming, how accurate do you want it to be?] (Number)
2 - X Value [What point do you want the derivative of?] (Number)
3 - Integrand [What function are you integrating?] (Function)
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.derivative(.01,6,function(x)
	return x^2
end)) -- This is evenly 12 since the derivative of x^2 is 2x, and 2*6 is 12

This function is equivalent to:

17) Summation/Product

Purpose
Find the sum/product over a set of terms in a specific pattern
Parameters
1 - Start Index [Where does the set of terms start?] (Number)
2 - End Value [Where does the set of terms end?] (Number)
3 - Function of x [What function of x will you be adding/multiplying together?] (Function)
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.summation(1,5,function(x)
	return x^2
end)) -- This is 55 1^2+2^2+3^2+4^2+5^2 = 1+4+9+16+25 = 55

This function is equivalent to:

For getting the product of a set of terms

local module = require(game.ReplicatedStorage.MathAddons)
print(module.product(1,3,function(x)
	return x^3
end)) -- This is 216 since 1^3*2^3*3^3 = 1*8*27 = 216

This function is equivalent to:

Removed Int Check from the documentation, if you really do want to use it, it's still inside the module. Optimized the fraction function from my own garbo algorithm to Fareys algorithm which zeroes in on a fraction based on whether it's greater or less than the guess. Sort of like a game of hot or cold.

[zCrxtix (zavier)]

Kinda late to the party, but cool module. Could you make a github repo?

[SamsAltAcc0unt]

@Squiegy

Intergration

It’s spelled “integration”.

You might want to double check some of the spelling.

[Squiegy (Squared)]

That’s on me! I should’ve double-checked spelling mistakes like that prior.

[Squiegy (Squared)]

Completely forgot to link it! Its in the original post above, or go to it here.

[Squiegy (Squared)]

Mathematical Constants

3 useless mathematical constants that serve no purpose in programming

18) Eulers Number

Purpose
Get the constant e

Proof (Math Rant)

Eulers Constant is calculated 2 ways

Infinite Sums

Using this sum

as k approaches infinity, you get better and better approximations for e, this isn’t what the module uses since this is very performance heavy

Compound Interest

An intuitive example for this would be the Compound Interest Formula

If you start with 1 dollar (P - Principal) and increase it by a rate of 100% (r - Rate) for 1 year (t - Time) n times, as n approaches infinity, you get better estimations for Eulers Constant
Lua is stupid so it comes up with 1 for numbers bigger than 10^15 (probably because lua doesn’t deal with numbers with more than 13 digits, this isn’t confirmed though)

The Final Way

Since solving it mathematically doesn’t work, I looked up a million digits of e and put them into the code

Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.e) -- This is approximately 2.71828182846

This value is approximately:

19) Pi

(This is literally just 162 digits but here you go)
Purpose
Get pi

Proof

Using Infinite Sums, you can use this formula

as k approaches infinity, the value of the sum gets closer to pi. This (thankfully) isn’t what the module uses since its a performance issue

Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.pi) -- This is about 3.14159265358979323846...

This value is approximately:

20) Phi / The Golden Ratio

Purpose
Get the Golden Ratio

Proof

Algebraicly

So (one of the things) the golden ratio has been defined as is that
(a+b)/a = a/b
b(a+b)/a = a
b(a+b) = a^2
ab + b^2 = a^2
a^2-ab-b^2
using the quadratic formula, a = (b±b*sqrt(5))/2
Since setting b to anything other than 1 would scale the function, giving an invalid answer. So it simplifies down to
a = (1±sqrt(5))/2, which is what phi is equal to

Rule 1

A rule states that ϕ- 1 is equal to 1/ϕ
so x-ϕ = 1/ϕ
ϕ^2-x = 1
ϕ^2-x-1 = 0
use the quadratic formula you get
ϕ = (1±sqrt(5))/2

Rule 2

This is sort of just an integration of the last rule, that
ϕ^2 = ϕ + 1
ϕ+1 = ϕ^2
1 = ϕ^2-ϕ
0 = ϕ^2-ϕ-1
use the quadratic formula you get
ϕ = (1±sqrt(5))/2

Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.phi) -- This is approximately 1.6180339887498948482045868343656381177203091798057628621354486227

This value is approximately:

And another useless function

15) Quadratic Solver

Purpose
Solve a math equation in the form of "ax^2+bx+c
Parameters
1 - Function (String)
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.equation('x^2+13x+40')) -- quadratic formula will give you x= -5 and x = -8

Real Situation
Imaginary

[Squiegy (Squared)]

New Functions - Factor Listing, L’Hôpital’s rule

Factor Listing - (New)

Purpose
Identify all the factors of an integer
Output
Table
Parameters
1 - Integer {number}
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.factors(24)) -- returns a table of all the factors, in this case it would be {1,2,3,4,6,8,12,24}

Real Situation
Split a server into a certain number of even groups

local module = require(game.ReplicatedStorage.MathAddons)
local teamCount = module.factors(#game.Players:GetPlayers())[math.random(#module.factors(#game.Players:GetPlayers()))]

Limits - (New)

More

L’Hôpital’s rule - Wikipedia

Purpose
Find the value of a function as it approaches the input
Output
Number
Parameters
1 - X Value [What is x approaching?] (Number)
2 - Function [What function are you getting the limit of?] (Function)
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.limit(6,function(x)
	return (x-6)^2/(x-6)
end)) -- there is a hole in the graph at the x value 6, but if simplified, this is supposed to be x-6, so 6-6=0. The limit of (x-6)^2/(x-6) as x approaches 6 is 0

This function is equivalent to:

• Reworked Quadratic Solver to return answers in LaTeX format

[Squiegy (Squared)]

Imaginary Library - (New)

• The goal for this function is to recreate every single math function, but support for input and outputs of imaginary numbers.

This is an ever growing library, so keep an eye out!
• How will this work?
The Complex Library is separated from the other functions and should be accessed like this

local complex = require(MathAddons).Imaginary

and using the functions is as easy as the parent library

local complex = require(MathAddons).Imaginary
local real,imaginary = complex.add(a,b,c,d) -- (a+bi)+(c+di)

The last parameter is telling the program whether you want it in string form, or to return two numbers

local complex = require(MathAddons).Imaginary
print(complex.add(1,2,3,4,false)) -- since the toggle is false (the default), it will return 4,6
print(complex.add(1,2,3,4,true)) -- this returns a string due to setting to true 4+6i
print(complex.add(1,2,3,4)) -- this will also return 4,6. So that calculating inputs of other functions will be easier

Addition of Complex Numbers

Purpose
Combine two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number

Parameters
1 - Number - a value in (a+bi)+(c+di)
2 - Number - b value in (a+bi)+(c+di)
3 - Number - c value in (a+bi)+(c+di)
4 - Number - d value in (a+bi)+(c+di)
5 - Bool - Returns a string or two
Examples

local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.addComplex(2,6,5,5)) -- a+bi+c+di = a+c+(b+d)i = 2+5+(6+5)i=7+11i, returns: 7,11

Multiplication of Complex Numbers

Purpose
Multiply two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number

Parameters
1 - Number - a value in (a+bi)(c+di)
2 - Number - b value in (a+bi)(c+di)
3 - Number - c value in (a+bi)(c+di)
4 - Number - d value in (a+bi)(c+di)
5 - Bool - Returns a string or two Numbers
Examples

local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.addComplex(2,6,5,5)) -- (a+bi)(c+di) = ac+bci+adi-bd = (ac-bd)+(bc+ad)i = 10-30+(30+10)i = -20+40i, returns -20,40

Divison of Complex Numbers

Purpose
Divide two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number

Parameters
1 - Number - a value in (a+bi)/(c+di)
2 - Number - b value in (a+bi)/(c+di)
3 - Number - c value in (a+bi)/(c+di)
4 - Number - d value in (a+bi)/(c+di)
5 - Bool - Returns a string or two Numbers
Examples

local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.divComplex(2,6,5,5)) -- = 0.8+0.4i returns .8,.4 

Work shown below

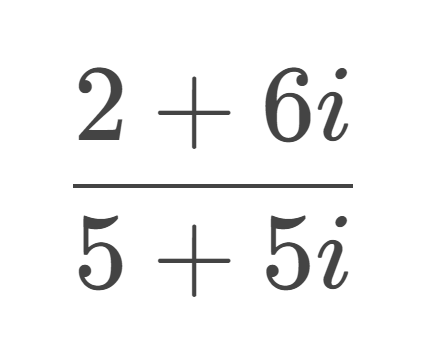
multiply the top and bottom by the conjugate of the denominator

simplify



final answer of .8+.4i

Conversion of Complex Numbers to their Polar Form

More

They give a very sciency proof and explanation of the polar form, let me simplify it
Polar Form - Wikipedia
Polar Form looks like this
where r is the radius of the circle the point is sitting on
and θ is the angle of the line
This is 1+1i plotted on the imaginary axis

The first step is to find the radius of the circle or in other words the length of the line
using the Pythagorean theorem
we can find the length of this line

a and b are both equal to 1 so
= 2
and c =
so the radius of that circle is
and if a circle is drawn, with radius you can see the point sits on that circle

to find the value θ, you need to find how far around the point is on the circle, or whats the degree of this angle

you need to use the arctangent function to find the given angle
the input will be the slope of the line, which is 1 since b/a = 1/1 = 1

so now we have the θ value, you can put it into the form and you get

Purpose
Combine two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number

Parameters
1 - Number - a value in (a+bi)
2 - Number - b value in (a+bi)
3 - Bool - Returns a string or two Numbers
Examples

local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.complexToPolar(1,1,true)) -- the example shown above gives us that 1+1i in polar form is approximately 1.4142135623730951e^0.7853981633974483i

Real to the power of i

More

I can’t find an explanation of this online, so here we go again
Two rules make the rest easy

applying the first rule

applying the second rule

now you can substitute any value for x to find the complex number

Purpose
find x^i for any value of x
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number

Parameters
1 - Number - x value in x^i
2 - Bool - Returns a string or two Numbers
Examples

local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.realToComplex(2,true)) -- returns 0.7692389013639721+0.6389612763136348i 

i to the power of a Real

More - Open at your own risk

Here’s an intuitive way i figured this out
here is what we know/the obvious
i^0 = 1
i^1 = i
i^2=-1
i^3=-i
i^4=1
these are also defined by 90-degree rotations on the imaginary axis

to get from 1 to i, you rotate 90 degrees (we’re adults now so we use pi/2)
so associating them with rotations we get
i^0 = 0pi/2
i^1 = pi/2
i^2 = 2pi/2
i^3 = 3pi/2
i^4 = 4pi/2 (or 0)
with this, we can make a unit rate
i^x=x*pi/2
now we can work with fractional values
since we’re working with i by itself, the radius is 1
the last part is to find a way to calculate the point of a power
for this, i used .5, or the square root of i

the point can be thought as legs of a right triangle and the hypotenuse is 1

sin is defined as the ratio of the opposite leg to the hypotenuse, but since the hypotenuse is 1, sin(x) is the length of the opposite side, in other words, to find the y value you get the sine of xpi/2 where x is the power, in the case of the example, x = .5
so the y coordinate = sin(.5pi/2) = sin(pi/4) which is
cosine in this context is defined as the ajecent leg, so the x value is cos(pi/4) =
so the coordinate of that point, or in other words the solution to i^.5 =

Purpose
find x^i for any value of x
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number

Parameters
1 - Number - x value in i^x
2 - Bool - Returns a string or two Numbers
Examples

local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.realToComplex(2,true)) -- returns 0.7692389013639721+0.6389612763136348i 

Complex Number to a Complex Number

More

There isn’t any explicit formula for this, only specific directions to get the answer, so i can only use an example

split the exponent, laws of exponents shows

we end up with

simplify

convert the base of the second factor into polar form (shown in the polar form category)

laws of exponents also shows that

so

convert into standard form

substitute it back in for into

rewrite the i^2 into -1

i will start rounding from here since it doesn’t get prettier from here on out

distribute

approximate again

you probably forgot about the first factor , now the final step is to multiply them

which equates to

which is close to the answer rounded to the nearest 13 places which is what the program will give

Purpose
Get the power of 2 complex numbers (a+bi)^(c+di)
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number

Parameters
1 - Number - a value in (a+bi)+(c+di)
2 - Number - b value in (a+bi)+(c+di)
3 - Number - c value in (a+bi)+(c+di)
4 - Number - d value in (a+bi)+(c+di)
5 - Bool - Returns a string or two Numbers
Examples

local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.pow(1,1,1,1,true)) -- the example shown above gives us that (1+1i)^(1+i)  is approximately 0.27395725383012104+0.5837007587586147i

[Squiegy (Squared)]

New Functions

---

This simultaneously replaced the linear equation solver.

Equation Solver

More

Newton’s Method - Wikipedia

Purpose
solve any equation that is equal to 0
Parameters
1 - Function [What function is equal to 0?] (Function)
Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.solver(function(x)
	return x^5-5*x+3
end)) -- returns a table containing -1.6180339887499, 1.27568220365099, 0.61803398874989

Updated Functions

---

Factorial now supports decimal inputs

Factorial

Purpose
Get the factorial of any number
Output
Number
Parameters
1 - Number

Examples

local module = require(game.ReplicatedStorage.MathAddons)
print(module.fact(5)) -- 5*4*3*2*1 = 120
print(module.fact(4.5)) -- ~52.3427777

Real Situation
You have a shelf stocking system, and you have 5 different itemodule, but only room for 3, you can calculate how many combinations the player can make

local module = require(game.ReplicatedStorage.MathAddons)
local itemodule = 5
local space = 3
script.Parent.Text = module.fact(itemodule)/(module.fact(space)*module.fact(itemodule-space)).. " possible combinations of itemodule" -- which will be 10 since 5!/(3!*(5-3)!) = 120/(6*2) = 10

New Look!

---

The documentation has been revamped to look more organized! Including a new FAQ section.


What’s next?

---

Statistics functions such as Standard Deviation, MAD, Median, and etc.