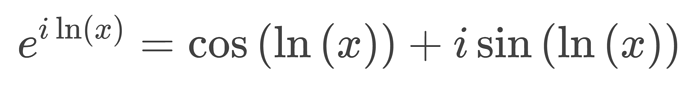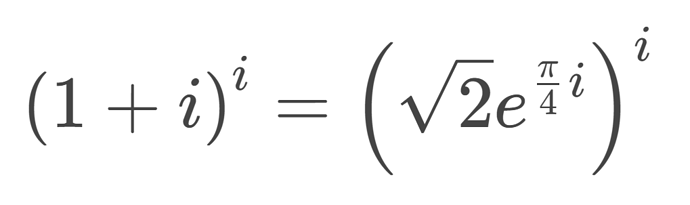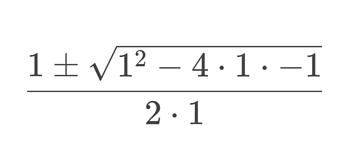Playground ||
Playground ||  Model ||
Model ||  Source
Source
What is MathAddons?
MathAddons is a simple yet useful module with math functions such as average, scientific notation, fraction conversion, and more!
Using any of the functions is as simple as:
-- Within a LocalScript or ServerScript and assuming MathAddons is placed in ReplicatedStorage
local Math = require(game.ReplicatedStorage.MathAddons)
local numbers = {1,2,3,4,5,6}
local average = Math.avg(numbers)
print(average) -- 3.5
FAQ
? What does MathAddons bring that the regular math functions don’t?
- ! This module contains 27 unique functions with different levels of complexity, from coinflips to integration.
? Is there a performance gap?
- ! I have yet to do the actual benchmarking, however, I will say some functions such as integration do rely on loops, other than the functions rely on a great amount of looping, they won’t have a noticeable performance impact.
? How frequently does this module get updated?
- ! There isn’t any schedule, it’s just when I learn/come up with a new math concept to add.
? Some of these functions are easy to make, why should I use them through a module?
- ! And to that I say you are perfectly justified thinking that way! I am making this module as a student as opposed to an expert. I try to remove simplistic functions or make them more useful and complex (They usually end up lacking any application). Working on this module is more or less of a fun hobby to me, people using it only make it more worthwhile updating!
? I have a function suggestion! Where can I submit it?
- ! You can reach me by messaging me or replying to this post!
? Do I need credit to use this module in a public project?
- ! Nope!
More frequently asked questions will be put here.
Applicable Functions
Round
Purpose
Round a number
Output
Number
Parameters
1 - number to round
2 - decimal point to round to (?)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.round(10.4)) -- 10
print(module.round(10.65)) -- 11
print(module.round(10.486,2)) -- 10.49
print(module.round(10.65,1)) -- 10.7
Real Situation
You have a currency with decimal places but you only want to round to the nearest hundredth
local module = require(game.ReplicatedStorage.MathAddons)
player.stats.Cash.Value = module.round(player.stats.Cash.Value,2) -- if the players cash value is 112.235, it will now be 112.24
Percentage
Purpose
Get the percentage of a decimal
Output
String
Parameters
1 - number to turn into percentage
2 - decimal point to round to (?)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.perc(.25)) -- 25%
print(module.perc(8/9,5)) --88.88889%
Real Situation
You make a game with an accuracy system, and want to show the accuracy in percentage
local module = require(game.ReplicatedStorage.MathAddons)
script.Parent.Text = "Accuracy: [" module.perc(hit/total).. "]"
Coin Flip
Purpose
Return true or false
Output
Boolean
Parameters
1- Odds of returning true [x% chance of getting true] (number from 0 to 100)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.flip(50)) -- 50 percent chance of true and false
print(module.flip(75)) -- 75 percent chance of true and 25 percent chance of false
Real Situation
Very straight-foward example, you want to randomly select players onto a team.
local module = require(game.ReplicatedStorage.MathAddons)
game.Players.LocalPlayer.stats.Team.Value = module.flip(50) and "Team1" or "Team2"
Factorial
Purpose
Get the factorial of any number
Output
Number
Parameters
1 - Number
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.fact(5)) -- 5*4*3*2*1 = 120
print(module.fact(4.5)) -- ~52.3427777
Real Situation
You have a shelf stocking system, and you have 5 different itemodule, but only room for 3, you can calculate how many combinations the player can make
local module = require(game.ReplicatedStorage.MathAddons)
local itemodule = 5
local space = 3
script.Parent.Text = module.fact(itemodule)/(module.fact(space)*module.fact(itemodule-space)).. " possible combinations of itemodule" -- which will be 10 since 5!/(3!*(5-3)!) = 120/(6*2) = 10
Thousands Separator
Purpose
Add thousands separators
Output
String
Parameters
1 - number
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.commaFormat(123456789)) -- 123,456,789
Real Situation
If your game is heavily revolved around numbers, and you don’t want ugly, unreadable numbers in your game.
local module = require(game.ReplicatedStorage.MathAddons)
script.Parent.Text = module.commaFormat(player.stats.Cash.Value) -- for example the player has 6212 cash, it'll show 6,212
Random
Purpose
Find a random number between the first value of the table and second, that is rounded to the second parameters decimal point
Output
Number
Parameters
1 - table {min,max}
2 - number to round to
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.random(1,10)) -- random integer value from 1-10
print(module.random({1,10},3)) -- random value from 1,10 rounded to the 3rd decimal point (or thousands place 10^3)
Real Situation
For example, you want a random rating generator, and lua only supplies integer values, but you want the 0-5 star ratings to have decimal values.
local module = require(game.ReplicatedStorage.MathAddons)
local starRating = module.random({0,5},1) -- can be 3.4 or 2.2 or 0.5
Factor Listing
Purpose
Identify all the factors of an integer
Output
Table
Parameters
1 - Integer {number}
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.factors(24)) -- returns a table of all the factors, in this case it would be {1,2,3,4,6,8,12,24}
Real Situation
Split a server into a certain number of even groups
local module = require(game.ReplicatedStorage.MathAddons)
local teamCount = module.factors(#game.Players:GetPlayers())[math.random(#module.factors(#game.Players:GetPlayers()))]
Average
Purpose
Returns the average of a table
Output
Number
Parameters
1 - table {number,…,number}
Examples
local module = require(game.ReplicatedStorage.MathAddons)
local t = {1,5,6,23,45,76,5,232,5,76,3,6,45,23,4,45,23,5}
print(module.avg(t)) -- 34.888888888889
Real Situation
For example you want an average level counter for a server
local module = require(game.ReplicatedStorage.MathAddons)
local t = {}
for i,v in pairs(game.Players:GetPlayers()) do
table.insert(t,v.stats.Level.Value)
end
local avg = module.avg(t)
Time
Purpose
Convert number from 0-24 to time format
Output
String
Parameters
1 - number
2 - boolean that toggles AM/PM format
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.time(13.25)) -- using 1 parameter would give you the 24 hour clock, this'll return "13:15"
print(module.time(13.25,true)) -- the second parameter is whether or not you want to use the 24 hour system or 12 hour. This'll return "1:15 PM"
Real Situation
You can convert the time of day in-game with this
local module = require(game.ReplicatedStorage.MathAddons)
print(module.time(game.Lighting.ClockTime,true)) -- for example the time is 14, itll return 2:00 PM
Prime Checker
Purpose
Returns true/false depending on whether an integer is prime
Output
Boolean
Parameters
1 - integer
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.prime(3)) -- since 3 cant be doesnt have any other factors other than 1 and itself, it returns true because its a prime
print(module.prime(24)) -- this will return false because 24 has more than 1 factor pair (6 and 4, 8, and 3, 12 and 2, 1 and 24.
Real Situation
A very niche idea but you can make a prime finder with this
local module = require(game.ReplicatedStorage.MathAddons)
for i,math.huge do
if module.prime == true then
print(i)
end
end
Convert to Fraction
Purpose
Converts numbers into fractions
Output
String
Parameters
1 - number
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.frac(.25) -- 1/4
print(module.frac(4/3) -- 4/3
I’m still working on efficiency since a for loop has to cycle through every single number to get to the exact one to work with the fractions, so try and stick to decimal spots from 1-6
Real Situation
A potential use would be also for an accuracy counter
local module = require(game.ReplicatedStorage.MathAddons)
script.Parent.Text = "Accuracy: [" module.frac(notesHit/TotalNotes).. "]"
Scientific Format
Purpose
Returns the input in scientific form
Output
If second parameter is false/nil, then string, otherwise a number
Parameters
1 - number
2 - any value that toggles e or exponential notation
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.science(3189263)) -- since there is no 2nd parameter, itll return 3.189263 * 10^6
print(module.science(3189263),'a') -- since the 2nd parameter isnt nil anymore it returns 3.189263e6
Real Situation
Turn big numbers into readable ones
local module = require(game.ReplicatedStorage.MathAddons)
local bigNum = 85123651283
local formatted = module.science(85123651283)
You can undo this function by using the module.rscience() function
local module = require(game.ReplicatedStorage.MathAddons)
local bigNum = 85123651283
local formatted = module.science(85123651283)
print(module.rscience(formatted)) -- returns 85123651283
Roman Numerals
Purpose
Convert integers into roman numerals
Output
String
Parameters
1 - integer
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.roman(5)) -- V
print(module.roman(12)) -- XII
print(module.roman(9)) -- IIV
Real Situation
You’re making a rank system every few levels they advance to a new rank, in those levels they progress in rank I, rank II, rank III, rank IV…
local module = require(game.ReplicatedStorage.MathAddons)
local rankTable = {'Noob','Okay', 'Good', 'Great', 'Pro', 'Advanced', 'Best', 'God Level'}
local level = 41
local levelsPerRank = 6
player.stats.Rank.Value = rankTable[math.floor(level/levelsPerRank)].. module.roman(level%levelsPerRank)
-- since 41/6 is 6 rounded down, the 6th index in the table is advanced, and 5 is left over, so the rank would be "Advanced V"
KMBT Format
Purpose
convert numbers into kmbt
Output
String
Parameters
1 - number at least 1000
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.kmbt(123456789)) -- 123.45M
print(module.kmbt(1234)) -- 1.23K
print(module.kmbt(1234567890123456789012345678901234567890)) --1.23Ddc
Real Situation
You have a currency system with large values
local module = require(game.ReplicatedStorage.MathAddons)
currency:GetPropertyChangedSignal('Value'):Connect(function()
script.Parent.Text = module.kmbt(currency.Value)
end)
Quadratic Solver (LATEX)
NOTE: If you’re only interested in the decimal values of the equation, use the solve function, this is for returning the solution in radical form (with imaginary values)
Purpose
Solve a math equation in the form of "ax^2+bx+c
Output
String or Number, String or Number
Parameters
1 - a value (number)
2 - b value (number)
3 - c value (number)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.quadsolve(1,13,40)) -- this is equal to "1x^2+13x+40", quadratic formula will give you x= -5 and x = -8
--Works the same way with imaginary numbers
print(module.quadsolve(1,10,40)) -- this is equal to "1x^2+10x+40", quadratic formula will give you x= -5+\sqrt{15}i and x = -5-\sqrt{15}i
Real Situation
Imaginary
Integration
More
Purpose
Get the integration of a given function with lower and upper bounds
Output
Number
Parameters
1 - Precision [There aren’t limits in programming, how accurate do you want it to be?] (Number)
2 - Lower Bound [Whats the lower bound of the integral?] (Number)
3 - Upper Bound [What’s the upper bound of the integral?] (Number)
4 - Integrand [What function are you integrating?] (Function)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.integral(.01,0,10,function(x)
return x^2
end)) -- This is approximately 1000/3 [333.83349999999007]
This function is equivalent to:

Derivatives
Purpose
Find the rate of change at a certain input of a function
Output
Number
Parameters
1 - Precision [There aren’t limits in programming, how accurate do you want it to be?] (Number)
2 - X Value [What point do you want the derivative of?] (Number)
3 - Integrand [What function are you integrating?] (Function)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.derivative(.01,6,function(x)
return x^2
end)) -- This is evenly 12 since the derivative of x^2 is 2x, and 2*6 is 12
This function is equivalent to:

Limits
Purpose
Find the value of a function as it approaches the input
Output
Number
Parameters
1 - X Value [What is x approaching?] (Number)
2 - Function [What function are you getting the limit of?] (Function)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.limit(6,function(x)
return (x-6)^2/(x-6)
end)) -- there is a hole in the graph at the x value 6, but if simplified, this is supposed to be x-6, so 6-6=0. The limit of (x-6)^2/(x-6) as x approaches 6 is 0
This function is equivalent to:

Summation/Product
Purpose
Find the sum/product over a set of terms in a specific pattern
Parameters
1 - Start Index [Where does the set of terms start?] (Number)
2 - End Value [Where does the set of terms end?] (Number)
3 - Function of x [What function of x will you be adding/multiplying together?] (Function)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.summation(1,5,function(x)
return x^2
end)) -- This is 55 1^2+2^2+3^2+4^2+5^2 = 1+4+9+16+25 = 55
This function is equivalent to:

For getting the product of a set of terms
local module = require(game.ReplicatedStorage.MathAddons)
print(module.product(1,3,function(x)
return x^3
end)) -- This is 216 since 1^3*2^3*3^3 = 1*8*27 = 216
This function is equivalent to:

Equation Solver
Purpose
solve any equation that is equal to 0
Parameters
1 - Function [What function is equal to 0?] (Function)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.solver(function(x)
return x^5-5*x+3
end)) -- returns a table containing -1.6180339887499, 1.27568220365099, 0.61803398874989
• The goal of this library is to recreate every single math function, but support for input and outputs of imaginary numbers.
This is an ever-growing library, so keep an eye out!
• How will this work?
The Complex Library is separated from the other functions and should be accessed like this
local complex = require(MathAddons).Imaginary
and using the functions is as easy as the parent library
local complex = require(MathAddons).Imaginary
local real,imaginary = complex.add(a,b,c,d) -- (a+bi)+(c+di)
The last parameter is telling the program whether you want it in string form, or to return two numbers
local complex = require(MathAddons).Imaginary
print(complex.add(1,2,3,4,false)) -- since the toggle is false (the default), it will return 4,6
print(complex.add(1,2,3,4,true)) -- this returns a string due to setting to true 4+6i
print(complex.add(1,2,3,4)) -- this will also return 4,6. So that calculating inputs of other functions will be easier
Addition of Complex Numbers
Purpose
Combine two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number
Parameters
1 - Number - a value in (a+bi)+(c+di)
2 - Number - b value in (a+bi)+(c+di)
3 - Number - c value in (a+bi)+(c+di)
4 - Number - d value in (a+bi)+(c+di)
5 - Bool - Returns a string or two
Examples
local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.addComplex(2,6,5,5)) -- a+bi+c+di = a+c+(b+d)i = 2+5+(6+5)i=7+11i, returns: 7,11
Multiplication of Complex Numbers
Purpose
Multiply two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number
Parameters
1 - Number - a value in (a+bi)(c+di)
2 - Number - b value in (a+bi)(c+di)
3 - Number - c value in (a+bi)(c+di)
4 - Number - d value in (a+bi)(c+di)
5 - Bool - Returns a string or two Numbers
Examples
local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.addComplex(2,6,5,5)) -- (a+bi)(c+di) = ac+bci+adi-bd = (ac-bd)+(bc+ad)i = 10-30+(30+10)i = -20+40i, returns -20,40
Divison of Complex Numbers
Purpose
Divide two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number
Parameters
1 - Number - a value in (a+bi)/(c+di)
2 - Number - b value in (a+bi)/(c+di)
3 - Number - c value in (a+bi)/(c+di)
4 - Number - d value in (a+bi)/(c+di)
5 - Bool - Returns a string or two Numbers
Examples
local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.divComplex(2,6,5,5)) -- = 0.8+0.4i returns .8,.4
Work shown below
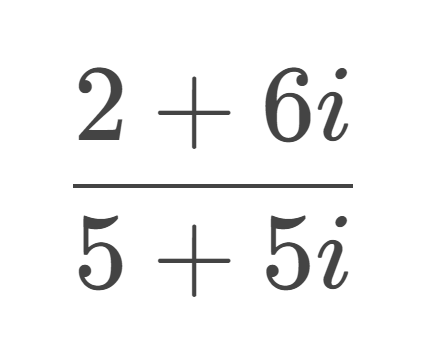
multiply the top and bottom by the conjugate of the denominator
simplify



final answer of .8+.4i
Conversion of Complex Numbers to their Polar Form
More
They give a very sciency proof and explanation of the polar form, let me simplify it
Polar Form - Wikipedia
Polar Form looks like this
where r is the radius of the circle the point is sitting on
and θ is the angle of the line
This is 1+1i plotted on the imaginary axis
The first step is to find the radius of the circle or in other words the length of the line
using the Pythagorean theorem
we can find the length of this line
a and b are both equal to 1 so ![]()
= 2
and c = ![]()
so the radius of that circle is ![]()
and if a circle is drawn, with radius ![]() you can see the point sits on that circle
you can see the point sits on that circle
to find the value θ, you need to find how far around the point is on the circle, or whats the degree of this angle
you need to use the arctangent function to find the given angle
the input will be the slope of the line, which is 1 since b/a = 1/1 = 1
so now we have the θ value, you can put it into the form and you get

Purpose
Combine two Complex Numbers
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number
Parameters
1 - Number - a value in (a+bi)
2 - Number - b value in (a+bi)
3 - Bool - Returns a string or two Numbers
Examples
local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.complexToPolar(1,1,true)) -- the example shown above gives us that 1+1i in polar form is approximately 1.4142135623730951e^0.7853981633974483i
Real to the power of i
More
I can’t find an explanation of this online, so here we go again
Two rules make the rest easy

applying the first rule

applying the second rule
now you can substitute any value for x to find the complex number
Purpose
find x^i for any value of x
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number
Parameters
1 - Number - x value in x^i
2 - Bool - Returns a string or two Numbers
Examples
local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.realToComplex(2,true)) -- returns 0.7692389013639721+0.6389612763136348i
i to the power of a Real
More - Open at your own risk
Here’s an intuitive way i figured this out
here is what we know/the obvious
i^0 = 1
i^1 = i
i^2=-1
i^3=-i
i^4=1
these are also defined by 90-degree rotations on the imaginary axis
to get from 1 to i, you rotate 90 degrees (we’re adults now so we use pi/2)
so associating them with rotations we get
i^0 = 0pi/2
i^1 = pi/2
i^2 = 2pi/2
i^3 = 3pi/2
i^4 = 4pi/2 (or 0)
with this, we can make a unit rate
i^x=x*pi/2
now we can work with fractional values
since we’re working with i by itself, the radius is 1
the last part is to find a way to calculate the point of a power
for this, i used .5, or the square root of i
the point can be thought as legs of a right triangle and the hypotenuse is 1
sin is defined as the ratio of the opposite leg to the hypotenuse, but since the hypotenuse is 1, sin(x) is the length of the opposite side, in other words, to find the y value you get the sine of xpi/2 where x is the power, in the case of the example, x = .5
so the y coordinate = sin(.5pi/2) = sin(pi/4) which is
cosine in this context is defined as the ajecent leg, so the x value is cos(pi/4) =
so the coordinate of that point, or in other words the solution to i^.5 =
Purpose
find x^i for any value of x
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number
Parameters
1 - Number - x value in i^x
2 - Bool - Returns a string or two Numbers
Examples
local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.realToComplex(2,true)) -- returns 0.7692389013639721+0.6389612763136348i
Complex Number to a Complex Number
More
There isn’t any explicit formula for this, only specific directions to get the answer, so i can only use an example

split the exponent, laws of exponents shows
we end up with
simplify
convert the base of the second factor into polar form (shown in the polar form category)
laws of exponents also shows that

so
convert
substitute it back in for
rewrite the i^2 into -1
i will start rounding from here since it doesn’t get prettier from here on out
distribute
approximate again

you probably forgot about the first factor
which equates to
which is close to the answer rounded to the nearest 13 places which is what the program will give
Purpose
Get the power of 2 complex numbers (a+bi)^(c+di)
Output
Parameter 5 set to true - String
Parameter 5 set to nil/false - Number, Number
Parameters
1 - Number - a value in (a+bi)+(c+di)
2 - Number - b value in (a+bi)+(c+di)
3 - Number - c value in (a+bi)+(c+di)
4 - Number - d value in (a+bi)+(c+di)
5 - Bool - Returns a string or two Numbers
Examples
local complex = require(game.ReplicatedStorage.MathAddons).Imaginary
print(complex.pow(1,1,1,1,true)) -- the example shown above gives us that (1+1i)^(1+i) is approximately 0.27395725383012104+0.5837007587586147i
• Some important constants (that still have no common use in programming)
Eulers Number
Purpose
Get the constant e
Proof (Math Rant)
Eulers Constant is calculated 2 ways
Infinite Sums
Using this sum

as k approaches infinity, you get better and better approximations for e, this isn’t what the module uses since this is very performance heavy
Compound Interest
An intuitive example of this would be the Compound Interest Formula

If you start with 1 dollar (P - Principal) and increase it by a rate of 100% (r - Rate) for 1 year (t - Time) n times, as n approaches infinity, you get better estimations for Eulers Constant
Lua is stupid so it comes up with 1 for numbers bigger than 10^15 (probably because lua doesn’t deal with numbers with more than 13 digits, this isn’t confirmed though)
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.e) -- This is approximately 2.71828182846
This value is approximately:

Pi
More
(This is just 162 digits but here you go)
Purpose
Get pi
Proof
Using Infinite Sums, you can use this formula

as k approaches infinity, the value of the sum gets closer to pi. This (thankfully) isn’t what the module uses since its a performance issue
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.pi) -- This is about 3.14159265358979323846...
This value is approximately:

Phi / The Golden Ratio
Purpose
Get the Golden Ratio
Proof
The definition of Phi is it being

split the first fraction into

simplify
b/a is the reciprocal of a/b, so they can be written as




using the quadratic formula to find the positive solution, you end up with
which is the golden ratio
Examples
local module = require(game.ReplicatedStorage.MathAddons)
print(module.phi) -- This is approximately 1.6180339887498948482045868343656381177203091798057628621354486227
This value is approximately:
What's Next
- String Calculator
- Parabola Vertex Calculator
- Quartile 1 & 3, Median, Interquartile Range, Range, Mode, MAD, Standard Deviation with Population & Sample
- More in the Imaginary Library
This is my first resource so I hope it helps 
I know this module is pretty easy to make in terms of the simplicity in (some of) the functions, but I thought it would be kinda cool to have an add-on to the default math functions. More things will come in the future so I recommend requiring the module by 7066695577