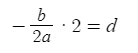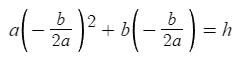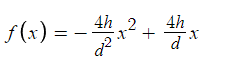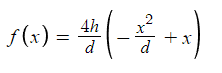Hello,
I wanted to derive a position based equation that helps me draw the path calculated when I’m using two points; start, and end (I have a function that calculates the vertex point):
local function getVertex(x0, x1, h)
local h = h or 0 -- height between the points
local up = Vector3.new(0,1,0)
local vector = (x1 - x0)
local midPoint = x0:Lerp(x1, 0.5)
local right = vector:Cross(up)--.Unit
right = right.Magnitude == 0 and Vector3.new(1,0,0) or right.Unit
local normal = right:Cross(vector)
normal = normal.Magnitude == 0 and up or normal.Unit
return midPoint + normal * h
end
local height = 10
local a = Vector3.new()
local c = Vector3.new(0,0,8)
local b = getVertex(a, c, height)
Although I have this graph and function above to guide me through a solution, I’m not too sure how I can convert the vertex equation into a 3D positional based equation using these three points, but I do know that these points are essential as I’m trying to mimic a trajectory-like curve (but not physics based, for peculiar reasons) to model out a positional function.
Where can I begin to tackle an approach to make up that positional function?
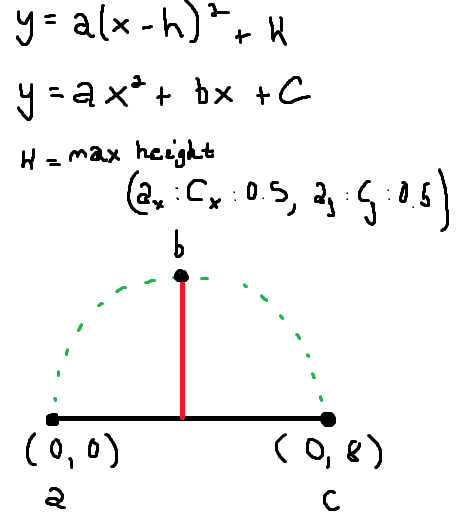

 !
!