Thank you for reporting! I overlooked that when copying between the minimum and maximum category.
Yeah its not only minimum and maximum, I remember multiple being like that. For example range uses the iqr function.
Update 1 - Imaginary Number Library
Sunday, June 19th, 2022
Statistics & Probability
Linear Regression
Purpose: returns the function (or slope & y intercept) and correlation coefficient of a data set
Parameters:
- As many data points as you please in the form of {x,y}
- The last parameter would be a boolean to Toggle Function Format
Output: Function, Number (If Function Toggle is false: Number, Number, Number
Explanation:
- *Calculates the line of best fit, and the correlation coefficient (the number that represents how good the line matches the set.
Example:
local slope, yint, r = module.linreg({0,2},{1,2},{2,3},{5,9},{6,5},{4,7},{10,5})
-- slope = 0.4142857142857143
-- yint = 3.057142857142857
-- r = 0.5385164807134504
local func, r = module.linreg({1,2},{5,8},{4,5},true)
-- r = 0.9607689228305227
local predictedPoint = func(10) -- predictedPoint = 14.23076923076923
Imaginary Library
These functions assist you when working with arithmetic on complex numbers. It gets unreal.
Before the you read the documentation below, do note what a valid complex number is:
local complexNum = {1,2} -- This represents 1+2i
local realNum = 2 -- this represents 2+0i, this is a valid input, same thing as {2,0}
local imaginaryNum = {0,5} -- this represents 0+5i, this is a valid input
local invalidinput = {5} -- this will return an error
local complex = module.Complex -- this is how you call the library
Note that most of these functions require an input of 2 tables, with two values each
Addition
Purpose: combine two complex numbers
Parameters:
- Table - {a,b}
- Table - {c,d}
- String Format Toggle (OPTIONAL) || Defaulted to false
Output: Table/String
Explanation:
- (a+bi)+(c+di) = (a+c)+(b+d)i
Example:
local
local x = complex.add({2,1},{0,3},true) -- x = '2+4i'
local y = complex.add({-5,1},4) -- y = {-1,1}
Multiplication
Purpose: multiply two complex numbers
Parameters:
- Table - {a,b}
- Table - {c,d}
- String Format Toggle (OPTIONAL) || Defaulted to false
Output: Table/String
Explanation:
- (a+bi)(c+di), you just distribute the binomial, anywhere you see an i^2, it becomes a -1 = ac-bd+(ad+cd)i
Example:
local
local x = complex.mul({2,1},{0,3},true) -- x = '-3+6i'
local y = complex.mul({-5,1},4) -- y = {-20,4}
Division
Purpose: divide two complex numbers
Parameters:
- Table - {a,b}
- Table - {c,d}
- String Format Toggle (OPTIONAL) || Defaulted to false
Output: Table/String
Explanation:
- (a+bi)/(c+di) multiply both sides by the conjugate as the numerator and denominator. you get (a+bi)(c-di)/(c+di)(c-di), which simplifies to (ac+bd+(bc-ad)i)/(c^2+d^2)
Example:
local
local x = complex.div({2,1},{4,3},true) -- x = '0.44+-0.08i'
local y = complex.div({-5,1},4) -- y = {-1.25,.25}
To Polar Form
Purpose: convert a rectangular value to polar
Parameters:
- Table - {a,b}
- String Format Toggle (OPTIONAL) || Defaulted to false
Output: Number, Number
Explanation:
- converting a rectangular form value to polar requires you to find the distance from the origin of the imaginary axis is that point: sqrt(a^2+b^2), and the angle if there was a line to be drawn from the origin to the point is the arctan(b/a)
Example:
local
local x = complex.toPolar({2,1},true) -- x = '2.23606797749979e^0.4636476090008061i'
local distance,theta = complex.toPolar({-5,1})
-- distance = 5.0990195135927845,
-- theta = -0.19739555984988078
From Polar Form
Purpose: convert a rectangular value to polar
Parameters:
- Number - Distance
- Number - Angle
- String Format Toggle (OPTIONAL) || Defaulted to false
Output: Table/String
Explanation:
- Converting polar form into rectangular form requires you to convert from polar form to Euler’s identity (re^iθ = r×cos(θ) + r×isin(θ), which can just be calculated using trig functions and arithmetic
Example:
local
local x = complex.fromPolar(2.23606797749979,0.4636476090008061,true) -- x = '2+1i'
local y = complex.fromPolar(5.0990195135927845,0.19739555984988078) -- y = {-5,1}
Exponentiation
Purpose: set a complex number to a power of a complex number
Parameters:
- Table - {a,b}
- Table - {c,d}
- String Format Toggle (OPTIONAL) || Defaulted to false
Output: Table/String
Explanation:
- Too tired to explain how this works, go check out the source code
Example:
local
local x = complex.pow({0,1},{0,1},true) -- x = '0.20787957635+0i' (This is actually i^i)
local y = complex.pow(3,3,true) -- y = '27+0i' (just 3^3)
local z = complex.pow({0,1},{2,0},true) -- z = '-1+0i' (this is i^2 which is defined as -1'
local a = complex.pow(-1,.5,true) -- a = '-1+0i' (this is i which is defined as sqrt(-1)', note that with powers less than 1, its important to know that there are more than 1 solutions to these powers, the module has to decide on 1)
Mandelbrot Checker
Purpose: Check if a complex number is in the mandelbrot set
Parameters:
- Table - {a,b}
- Number - Power (OPTIONAL) || Defaulted to 2
Output: Boolean
Explanation:
- This requires a bit of representation
Images
This below is the mandelbrot set
everything inside of it is a solution, so inputing any complex number inside the set will return true
What is the second parameter you ask?
Well, the mandelbrot set is generated by iterating this function an infinity amount of times
z = 0
z = z^2+c
where the z starts at 0 and c is the input. then z is equal to whatever the solution to 0^2+c is, and you repeat the process of subsituting whatever the output was back into z.
The second parameter is the power, you can tell in the equation that the set has the highest power of 2, the second parameter changes that number
Power of 3

Power of 4

Power of 5

Power of 6

With this function, you can actually generate these sets
and with a bit of modification to the function, you can get very detailed
and yes, even with different powers
How the function determines if something is in or out of the set, if checking if the real part of z to the power of 2 plus the imaginary part to the power of 2 is less than 4, if it is than its apart of the set, else, it isnt
Example:
local
local x = complex.mandelbrot({0,1},2) -- x = true
local y = complex.mandelbrot({0,1},4) -- x = false
local z = complex.mandelbrot({-2,0}) -- x = true
- Some mistakes in the example code such as incorrect function names, thanks to
@bitsplicer for bringing this to my attention
Thank you for all the support on this module 
Wow, this looks really useful, and will definitely consider installing it in my game!
this my good sir is what i would call a banger
good stuff!!! super proud 
Man that is pretty cool. I do not even think that the calculus functions are useless. In fact I was able to approximate pi up to 7 decimal digits correct with just three lines of code :
local Math = require(game.ReplicatedStorage.MathAddons)
s = 2 * Math.integral(-1,1, function(x) return math.sqrt(1-x^2) end)
print(s)

For anyone interested in math here is why this works:
Assume we have a circle with radius 1. Its area is then the following: pi * r^2 = pi * 1 = pi
So, by knowing the area of such a circle we can theoretically calculate pi. We also know that there is a function that describes the curve of the half of the circle which in our case is the following:
Thus if we can find the area of the region between the points -1 and 1 and multiply it by two we can then find the area of our whole circle which in our case is equal to pi. How can we do this? Luckily for us there is the first fundamental theorem of calculus which states that
Let f(x) be a continuous positive function between a and b and consider the region below the curve y = f(x), above the x-axis and between the vertical lines x = a and x = b. Then denote the area of this region by
and call this the definite integral of f(x) from a to b.
We know our function which is y=f(x)=sqrt(1-x^2) and our points a and b are -1 and 1 respectively. Thus the area under the curve is :

The problem with this though is that the indefinite integral of sqrt(1-x^2) is the following:
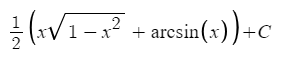
Now, you will ask what is the problem with the above? The answer is that the arcsin formula is the following:
arcsin(x) = π/2 - arccos(x) So as you understand we can not find pi using pi because we will end in something like this 0=0. Now, you might ask, how did the above module calculate pi ? The answer is that it did not calculate it, but it approximated it with the following method:
As you can see, the integral function does the following things:
First it makes sure that the parameters are in fact two numbers and a function. Then it checks whether the upper bound is less than zero and if it is, it takes the absolute value of it. In our case the upper bound is equal to one so there is no need to take its absolute value. Next, it does the following thing:
s = sqrt(1-(-1))^2 * 1e-5 + sqrt(1-1^2)*1e-5 + sqrt(1-(1e-5)^2)*1e-5 which then becomes
s = 0 + 0 + sqrt(1-(1e-5)^2) * 1e-5 which when multiplied by two is an approximation of our area and hence of pi.
I have to admit that the methods that are used in both calculus functions are smart because in reality these seemingly random numbers (1e-12) and (1e-5) are small changes(which is exactly what calculus examines, changes) that will approximate the result.
Great work, mate! Would you consider adding a function to convert a string to an equation and an equation to a string?
Input: “3 + 3” OR 3 + 3
Output: 3 + 3 OR “3 + 3”
I was actually planning to make this with the previous version before my previous account was terminated, definitely will work on this next!
I remember I tried to make a pi generator with lebreniz formula. And it was innacurate as hell. Thank you for this.
By the way, in the integral function, you can lower the number “1e-5” so something like 1e-8, the function will take longer to run since its a loop, however this will get you better estimates of pi, or whatever you’re attempting to calculate
Hi, it’s me again. I tried doing some optimizations on your Solver function, and I managed to shave off a considerable amount of processing time.
Standalone module of the function with my changes
local module = {}
type math = (number) -> (number)
local flr = math.floor
local ts = tostring
local strL = string.lower
local inf = math.huge
function round(n: number, decimal: number?): number
local factor: number = decimal or 1
return flr(n * factor + .5) / factor
end
function module.Solve(f: math, iterations: number?): {number} --2nd parameter allows for user-set amount of iterations
local iterations = iterations or 1e3 --default iteration amount of 1000
local t: {number} = {}
for i = -20, 20, .1 do
table.insert(t, i)
end
for ii = 1, iterations do
for i, a in ipairs(t) do
local fa: number = f(a)
local num: number = a - 1e-5*fa / (f(a + 1e-5) - fa)
local num2: number = round(num, 1e14)
t[i] = if strL(ts(num2)) == 'nan' then inf else if ii == iterations then num2 else num
end
end
local bl: {true} = {}
local n: {number} = {}
for _, v in ipairs(t) do
local num: number = round(v, 1e10)
if not bl[num] then
bl[num] = true
table.insert(n, num)
end
end
table.sort(n)
return n
end
return module
As for actual output, it’s basically the same. The loss of precision should be negligible for any practical applications.
Edit 2: made some more changes to the script for even more performance
I definitely overlooked performance when making the function, this will be apart of the next version of the module. Thanks for the help once again!
Update 2 - Miniscule Updates & a new module
Thursday, June 30th, 2022
Algebra
Lambert W function
Purpose: find the value of x for an equation in the form of x*e^x when its equal to some number y
Parameters:
- Number - y
Output: Table
Explanation:
-
This uses the solver function
Lambert W function - Wikipedia
Example:
local x = module.lambert(5*math.exp(5)) -- x = 5
local y = module.lambert(3*math.exp(3)) -- y = 3
local z = module.lambert(2) -- z = 0.8526055020137
Imaginary Library
To Array
Purpose: convert a number (complex or not) to an array in the form of {a,b} from the form “a+bi”
Parameters:
- String/Number
Output: Table
Explanation:
- “1+i” will convert to {1,1}, “5-2i” will convert to {5,-2}, “i” converts to {0,1}, this is a general idea
Example:
local x = complex.toArray("1+i") -- x = {1,1}
local y = complex.toArray("5-2i") -- y = {5,-2}
local z = complex.toArray("i") -- z = {0,1}
To String
Purpose: convert an array to an string/number in the form of “a+bi” from the form {a,b}
Parameters:
- Table
Output: String/Number
Explanation:
- {1,1} will convert to “1+i”, {5,-2}will convert to “5-2i” , {0,1} converts to “i”, this is a general idea
Example:
local x = complex.toString({1,1}) -- x = "1+i"
local y = complex.toString({5,-2}) -- y = "5-2i"
local z = complex.toString({0,1}) -- z = "i"
- Solver function was very inefficient, thank you @Prototrode for bringing this to my attention and offering an improved version of the function
- There were calls to print random variables scattered around the module due to debugging, those are all removed
- Addition and Multiplication with complex values now support more than two inputs, these inputs can also be strings such as “1-2i” or “i”
- All imaginary library functions that return a complex value, will now be more readable when the imaginary term has a negative coefficient, thanks to the toString and toArray functions.
Before: "9+ -33i"
Now: "9-33i"
Ive created a new module for graphing functions called Graphit which allows you to graph any function you’d like.
Update 3 - More Complex Number Support
Saturday, July 2nd, 2022
Algebra
Tetration
Purpose: calculate x^x, a certain amount of times
Parameters:
- Number -
- Iteration Count - how many times is x taken to the xth power (OPTIONAL) || Defaulted to 2
Output: Number/Table
Explanation:
-
if you input 5,2 as the parameters, it will return 5^5, if you input 2,4, it will return 2^2^2^2.
Heres more on tetration:
Tetration - Wikipedia
Example:
local x = module.tetration(math.sqrt(2),10000) -- x = 2 -- fun fact the infinite tetration of root 2 is 2!!
local y = module.tetration(3) -- y = 3^3=27
local z = module.tetration(i,10000) -- z = 0.43828293672702395+0.3605924718713796i
Imaginary Library
To Real
Purpose: convert a complex number into its real part
Parameters:
- Number
Output: String/Number
Explanation:
- The real part of 1+i is 1, so it returns 1
Example:
local x = complex.Re(1+i) -- x = 1
local y = complex.Re(5-2*i) -- y = 5
local z = complex.Re(i) -- z = 0
To Imaginary
Purpose: convert a complex number into its imaginary part
Parameters:
- Number
Output: String/Number
Explanation:
- The imaginary part of 1+2i is 2, so it returns 2
Example:
local x = complex.Im(1+i) -- x = 1
local y = complex.Im(5-2*i) -- y = -2
local z = complex.Im(i) -- z = 1
Ive updated the module so that common math functions are compatible with inputs and outputs of complex numbers
- Sine (sin)
- Cosine (cos)
- Tangent (tan)
- Arcsine (asin)
- Arccosine (acos)
- Arctangent (atan)
- Sine Hyperbolic (sinh)
- Cosine Hyperbolic (cosh)
- Tangent Hyperbolic (tanh)
- Logarithm - The base and argument can be complex and/or negative (log)
- Power (pow)
- Square Root (sqrt)
And also makes some normal functions compatible with complex numbers
- Nth Fibonacci Number (fibonacci)
- Summation/Product (summation/product)
- Vertex Calculator (vertex)
- Tetration (tetration)
- Now, you can use i as if its a number, to call it, you can do:
local i = module.Complex.i
print(i^2) -- -1
We are all gathered here to witness the removal of several complex number functions
- Addition - Due to now i being a datatype, adding is as simple as 1+i
- Multiplication - For the same reason as Additions removal
- Division - Same reason
I dont know what the next update should have, let me know if you have an idea! 
It would be helpful if you mentioned some functions (especially the one in the statistics and probability section) mutates the table pointer especially if I expect it to not mutate (MathFunctions.min, MathFunctions.max).
print(MathAddons.min({0, -0}))
print(MathAddons.min({-0, 0}))
prints 0 and -0 rather than -0 and -0. Was this intentional?
MathAddons.mode actually returns a string
print(type(MathAddons.mode({ 1 })[1]))
even though the documentation stated that the function returns tables of numbers (IEEE).
I don’t think formatting belongs in math. I don’t recommend parsing formatted string (inverse format strings) as formatting is supposed to display numbers and parsing numbers that’s only supposed to show in the UI feels weird to me. What’s your motivation of the parsing functions - fromComma, fromKMBT, fromNumeral, etc?
The semantics is also an issue.
toKMBT return a number for values below ±1000 yet in the docs it’s stated that it returns a string?
print(MathAddons.toKMBT(1) == 1)
prints true. This is a serious bug in my opinion, as using string methods could error saying attempting to index number value.
toComma disregards signed zeroes.
ToFraction also prints 2^-1022 incorrectly as 1/20001 false, and did not simplify the denominator of 2^53 when finite IEEE 754 binary64 values is a subset rational with the denominator of 2^k.
print(Math.ToFraction(2 ^ -1022))
print(Math.ToFraction(2 ^ 53))
the first is not even a close approximation, and in the second, the denominator could be simplified to 9007199254740992/1.
Can I ask what’s the point of MathAddons.pi when math.pi already exists? Adding more digits doesn’t make it any more precise:
MathFunctions.pi = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555
as math.pi is 0x1.921fb54442d18p1 which is represented in IEEE 754 binary64 as 0 10000000000 1001001000011111101101010100010001000010110100011000 and at a VM-level the number data type in Luau is IEEE 754 binary64 in Roblox.
I noticed that you used pairs on tables with only ordinal indices, do note that as pairs has the same behaviour as next, the order of pairs and next is explicitly undefined. You should use ipairs or generalized iteration instead.
I think semantics of many (or majority) of these is something you should improve in your library.
Thanks for the feedback,
Not necessarily intentional but not a bug either, normal math functions like math.min and math.max behave the same way,
print(math.min(0,-0)) -- = 0
print(math.min(-0,0)) -- = -0
print(math.max(0,-0)) -- = 0
print(math.max(-0,0)) -- = -0
this is just how table.sort functions, having -0 deemed greater than 0 is not an actual problem, since when being compared to non 0 numbers, they will function normally since -0 is equal to 0, and order wont matter.
This was my mistake! I forget that although you can still do and inequalities on numbers in forms of strings, that they wouldn’t remain strings. This will be patched in the next update.
These functions are more applicable compared to other functions, although they perform no actual manipulation or computation of the input, there still is math behind it.
This also will be fixed in the next update.
The module runs a loop which plays a game of hot or cold to guess the fraction, it runs a loop of 20,000 times to get the best approximation possible. for numbers less than 1/20001
I have fixed this however, now the function will scale the input so it becomes larger than 1/20001, this is what the new values now are
print(Math.ToFraction(2 ^ -1022)) -- = 174619484/7.84780619e315
print(Math.ToFraction(2 ^ 53)) -- = 9007199254740992/1
I’m not sure why you would need the first one in any case since any number with over 308 digits is just considered math.huge,
print(1/math.huge) -- = 0
You make a point, this will be removed in the coming update
This doesn’t make any real difference in the code, however this does seem safer to use in case something does get sorted incorrectly.
I appreciate the criticism, most of your suggestions will be implemented in the next update.
Update 4 - Minor Changes
Saturday, July 9th, 2022
- The mode function now returns a table of numbers, instead of strings
- Most formatting functions now return string outputs when
-1000 < x < 1000 - Fraction function now supports numbers smaller than
1/20001 - Solver function now supports being set equal to two functions
f(x) = g(x), solve for x
- Pi -
math.pi
Small personal update regarding the module, yesterday my pc overheated (from Roblox haha) and is refusing to turn on. I may have to buy a new one if the circumstances don’t change, which may take a while considering my budget and specifications I need.
To sum it up the next update for the module is probably in september.
(typing from my phone so disregard the organization)
This is an amazing module, still wondering. Has it been updated and/or are you still maintaining it?
sorry for bump
thanks, and it isnt dead! there will be a few more functions coming out like prime factorization, logical operations like xor, nCr, and others things which are only good for mathematical use.
Im still here taking suggestions just i dont have the same time as i did in the summer when i was out of school











