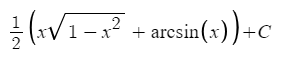MathAddons+ is a simple yet large module for all your mathematical needs
With over 85 functions, such as calculating the mean, scientific notation, fraction conversion, and more!
Using any of the functions is simple:
local Math = require(game.ReplicatedStorage.MathAddons)
local numbers = {1,2,3,4,5,6}
local average = Math.avg(numbers)
print(average) -- 3.5
Keep in mind that some functions aren’t as beginner-friendly as coin flip and average, functions such as integration and base conversion require reading the documentation below to understand what each parameter represents.
Questions that may be asked
? What does MathAddons bring that regular math functions don’t?
- ! This module has 50 math functions that aren’t seen in the regular math library.
? Is there a noticeable performance difference between this module and the math library?
- ! I will say some functions such as integration do rely on loops, other than the functions rely on a great amount of looping, however, they won’t have a noticeable performance impact.
? Does this module get updated frequently?
- ! There is no specific schedule, it really depends on what I discover.
? Some of these functions are easy to make, why should I use them through the module?
- ! There isn’t any big motivation for this module to be used, working on this module is just a hobby to me
? I have a function suggestion! Where can I submit it?
- ! You can reach me by messaging me or replying to this post!
? Do I need credit to use this module in a public project?
- ! Credit is appreciated but absolutely not necessary!
Statistics and Probability
The functions that are usually used to calculate probabilities and make educated guesses.
Flip
Purpose: create a random chance
Parameters:
- Number from 0-1, which represents a 0-100% chance
Output: Boolean
Explanation:
- If your chance is .5, you have the same chance of getting true as false. If your chance is .85, you are likely to return true, but uncertain. If your chance is .15, you are likely to return false.
Example:
local x = module.flip(.5) -- x is true or false due to a 50-50 chance
local y = module.flip(.98) -- y is likely going to be true due to a 98% chance
local z = module.flip(.01) -- z is most likely going to be false due to a 1% chance
Standard Deviation
Purpose: Calculate the Standard Deviation of a Data Set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
- Toggle the Population/Sample Deviation with a Boolean (OPTIONAL) || Defaulted to false
Output: Number
Explanation:
- This function returns a number representing a measure of how dispersed the data is about the mean. The larger it is, the less predictable the data set is.
I can leave some links below since I don’t fully understand this weird formula. The second parameter is optional and defaulted to false (Sample Deviation)
Standard deviation - Wikipedia
Example:
local x = module.sd({86,84,85,93,86}) -- x = 3.56370593624, this number is this high (meaning unpredictable) because of the outlier 93.
local y = module.sd({86,84,85,86}) -- y = 0.957427107756, much lower and predictable because there is no more outlier.
Minimum
Purpose: return the smallest value in a table
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- Self-explanatory, this returns the smallest value from a table
Example:
local x = module.min({2,3,4,5,2,2,0,5}) -- x = 0 since its the smallest value.
local y = module.min({2,3,4,5,2,2,5}) -- y = 2 since 0 was removed and 2 is the next smallest number.
Quartile 1
Purpose: returns the first quartile value of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- returns the number that’s 25% of the way in the dataset, a few more rules apply but this is a general idea
Example:
local x = module.q1({2,3,4,5,1,2,2,0,5}) -- x = 1.5
local y = module.q1({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = 4
Median
Purpose: returns the median of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- returns the middle number in a dataset (when sorted from least to greatest)
Example:
local x = module.median({2,3,4,5,1,2,2,0,5}) -- x = 2
local y = module.median({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = 5
Quartile 3
Purpose: returns the third quartile value of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- returns the number that’s 75% of the way in the dataset, a few more rules apply however, this is a general idea
Example:
local x = module.q3({2,3,4,5,1,2,2,0,5}) -- x = 4.5
local y = module.q3({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = 7
Maximum
Purpose: return the largest value in a table
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- Self-explanatory, this returns the largest value from a table
Example:
local x = module.max({2,3,4,5,2,2,0,5}) -- x = 5 since its the largest value.
local y = module.max({2,3,4,2,2,0}) -- y = 4 since 5 was removed and 4 is the next largest number.
IQR
Purpose: returns the IQR of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- returns the difference of the third quartile to the first
Example:
local x = module.iqr({2,3,4,5,1,2,2,0,5}) -- x = 3
local y = module.iqr({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = 3
Range
Purpose: returns the range of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- returns the difference of the maximum to the minimum
Example:
local x = module.range({2,3,4,5,1,2,2,0,5}) -- x = 5
local y = module.range({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = 6
Mode
Purpose: returns the mode of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Table of numbers
Explanation:
- returns which data value appears the most in the data set
Example:
local x = module.mode({2,3,4,5,1,2,2,0,5}) -- x = {2} (it appears 3 times)
local y = module.mode({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = {5,4} (they appear the same amount of times)
MAD
Purpose: returns the MAD of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- returns the average of the differences from each data value to the mean. the larger number shows that data values are far from the mean, meaning there is a large difference above and below the mean. A lower number means the values are closer together
Example:
local x = module.mad({2,3,4,5,1,2,2,0,5}) -- x = 1.4074074074074074
local y = module.mad({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = 1.611111111111111
Average
Purpose: returns the average of a data set
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- Adds up all the numbers in the data set and divides the sum by how many values there are
Example:
local x = module.avg({2,3,4,5,1,2,2,0,5}) -- x = 2.666666666666667
local y = module.avg({5,3,4,4,7,8,5,4,3,5,7,9}) -- y = 5.333333333333333
Z Score
Purpose: returns the Z score of a dataset
Parameters:
- Table in the form of {a,b,c…} where all the values inside are numbers
Output: Number
Explanation:
- The Z score is a value that represents how many standard deviations a data point is from the mean
Example:
local x = module.zscore({2,3,4,5,1,2,2,0,5}) -- x = {
["0"] = -1.539600717839002,
["1"] = -0.9622504486493764,
["2"] = -0.3849001794597506,
["3"] = 0.1924500897298751,
["4"] = 0.7698003589195008,
["5"] = 1.347150628109127}
local y = module.zscore({5,3,4,4,7,8,5,4,3,5,7,9},true) -- y = {
["3"] = -1.184755600676077,
["4"] = -0.6770032003863299,
["5"] = -0.1692508000965824,
["7"] = 0.8462540004829127,
["8"] = 1.35400640077266,
["9"] = 1.861758801062408}
Linear Regression
Purpose: returns the function (or slope & y intercept) and correlation coefficient of a data set
Parameters:
- As many data points as you please in the form of {x,y}
- The last parameter would be a boolean to Toggle Function Format
Output: Function, Number (If Function Toggle is false: Number, Number, Number
Explanation:
-
Calculates the line of best fit, and the correlation coefficient (the number that represents how good the line matches the set.
Example:
local slope, yint, r = module.linreg({0,2},{1,2},{2,3},{5,9},{6,5},{4,7},{10,5})
-- slope = 0.4142857142857143
-- yint = 3.057142857142857
-- r = 0.5385164807134504
local func, r = module.linreg({1,2},{5,8},{4,5},true)
-- r = 0.9607689228305227
local predictedPoint = func(10) -- predictedPoint = 14.23076923076923
Factorial/Gamma
Purpose: Returns x!
Parameters:
- Number
Output: Number
Explanation:
-
5! = 120 because 5×4×3×2×1
Example:
local x = module.factorial(5) -- 120
local y = module.factorial(.5) -- 0.8862269254527584
local z = module.factorial(module.Complex.i) -- 0.49801566812031056-0.15494982830241888i
local a = module.factorial(-2.3) -- 3.3283470067886083
-- module.gamma(x) = module.factorial(x-1)
nCr
Purpose: returns the amount of ways to select a group of items where the order of the items does not matter.
Parameters:
- Amount of items
- Amount of items being selected
Output: Number
Explanation:
-
The formula for nCr is n!/(r!×(n-r)!).
Example:
local x = module.nCr(5,3) -- 10
local y = module.nCr(12,4) -- 495
nPr
Purpose: returns the amount of ways to select a group of items where the order of the items does matter.
Parameters:
- Amount of items
- Amount of items being selected
Output: Number
Explanation:
-
The formula for nPr is n!/(n-r)!.
Example:
local x = module.nPr(5,3) -- 60
local y = module.nPr(12,4) -- 11880
Pascals Triangle
Purpose: Returns a given row of the pascals triangle
Parameters:
- Row
Output: Number
Explanation:
-
Pascals triangle is generated by adding two numbers on the top row and bringing it down a row, for example row with 1 2 1; 0+1 = 1, 1+2 = 3, 2+1 = 3, 1+0 = 1. So 1 3 3 1 becomes the next row

Example:
local x = module.pascalstri(5) -- {1, 5, 10, 10, 5, 1}
local y = module.pascalstri(3) -- {1, 3, 3, 1}
GCD
Purpose: returns the GCD of a data set
Parameters:
- Number
- Number
Output: Number
Explanation:
- Calculates the number which can divide evenly into both parameters
Example:
local x = module.gcd(45,10) -- x = 5
local y = module.gcd(63,14) -- y = 7
LCM
Purpose: returns the LCM of a data set
Parameters:
- Number
- Number
Output: Number
Explanation:
- Calculates the smallest number which the two parameters can both divide into
Example:
local x = module.lcm(45,10) -- x = 90
local y = module.lcm(63,14) -- y = 126
Floor
Purpose: rounds a number down to the nearest decimal (d)
Parameters:
- Number - Number to round down
- Number - Decimal place to round down to
Output: Number
Explanation:
- rounds a number down to the nearest nth decimal, if the 2nd parameter is 2, the number can look like 3.14 but not 3.1415
Example:
local x = module.floor(3.141592653589,3) -- x = 3.141
local y = module.floor(2.7182818,0) -- y = 2
local z = module.floor(2.7182818,-1) -- z = 0 (2 rounded down to the nearest 10 is 0
Round
Purpose: rounds a number to the nearest decimal (d)
Parameters:
- Number - Number to round
- Number - Decimal place to round to
Output: Number
Explanation:
- rounds a number to the nearest nth decimal, if the 2nd parameter is 2, the number can look like 3.14 but not 3.1415
Example:
local x = module.round(3.141592653589,3) -- x = 3.142
local y = module.round(2.7182818,0) -- y = 3
local z = module.round(2.7182818,-1) -- z = 0 (2 rounded to the nearest 10 is 0
Ceil
Purpose: rounds a number up to the nearest decimal (d)
Parameters:
- Number - Number to round up
- Number - Decimal place to round up to
Output: Number
Explanation:
- rounds a number up to the nearest nth decimal, if the 2nd parameter is 2, the number can look like 3.14 but not 3.1415
Example:
local x = module.ceil(3.141592653589,3) -- x = 3.142
local y = module.ceil(2.7182818,0) -- y = 3
local z = module.ceil(2.7182818,-1) -- z = 10 (2 rounded up to the nearest 10 is 10
Factor Listing
Purpose: list the factors of a number
Parameters:
- Integer
Output: Table
Explanation:
- List the numbers that divide evenly into the input
Example:
local x = module.factors(60) -- x = {1,2,3,4,5,6,10,12,15,20,30,60}
local y = module.factors(29) -- y = {1,29}
local z = module.factors(16) -- z = {1,2,4,8,16}
Function Iteration
Purpose: Iterate a function for a given input, a given amount of times
Parameters:
- Number
- Integer - Iteration Amount
- Function
Output: Number
Explanation:
- Iterate through a function for some number of times, after each iteration, the output of the last becomes the input for the next (note, the input usually doesn’t matter if the rate of change is from -1 to 1 at some point
Example:
local x = module.iteration(5,100,function(x) return math.cos(x) end) -- x = 0.7390851332151607
local y = module.iteration(-2,200,function(x) return .25^x end) -- y = 0.5
Nth Root
Purpose: gets the nth root of the radicand
Parameters:
- Number
- Number - Index
Output: Number
Explanation:
- just x^(1/y)
Example:
local x = module.nthroot(16,4) -- x = 2
local y = module.nthroot(729,9) -- y = 3
Nth Fibonacci Number
Purpose: find the nth term in the Fibonacci sequence, can find complex values too
Parameters:
- Number/Table in the form {a,b}
Output: Integer
Explanation:
- The fibonacci sequence is a famous sequence where the first and second term are 1 & 1, and you add those digits to get the next term
1,1,2,3,5,8,13,21,24,55,89,144…
Theres a very funky looking explicit formula that also gets this sequence, however you can insert fractional values into the function to complex complex results, using the complex power function, you can obtiain the complex results
Example:
local x = module.fibonacci(5) -- x = 5
local y = module.fibonacci(15) -- y = 610
local z = module.fibonacci(.5) -- z = '0.568864481-0.35157758425529523i'
local a = module.fibonacci(1+i) -- z = '0.6520177626+0.32939575714235453i'
Nth Lucas Number
Purpose: find the nth term in the Lucas numbers
Parameters:
- Integer
Output: Integer
Explanation:
- The Lucas numbers is a famous sequence where the first and second terms are 2 & 1, and you add those digits to get the next term
2,1,3,4,7,11,18,29,47,76…
Example:
local x = module.lucas(5) -- x = 7
local y = module.lucas(15) -- y = 843
local z = module.lucas(-6) -- z = -29
Formatting
The functions used for easy readability of numbers
All of these functions have their inverses and they’re used like this:
local x = module.toComma(12345678) -- 12,345,678
local y = module.fromComma('12,345,678') -- 12345678
Any function with a suffix of to has its inverse with a suffix of from
The input of all inverse functions are strings, and their outputs are always numbers
To Comma
Purpose: convert insert commas between digits for easier readability
Parameters:
- Number
Output: String
Explanation:
- This puts a comma between every 3 digits
Example:
local x = module.toComma(2938645938) -- x = 2,938,645,938
local y = module.toComma(125) -- y = 125
local z = module.toComma(-123456.5) -- z = -123,456.5
Inverse Example:
local x = module.fromComma('2,938,645,938') -- x = 2938645938
local y = module.fromComma('125') -- y = 125
local z = module.fromComma('-123,456.5') -- z = -123456.5
To KMBT
Purpose: ends a number in the first letter(s) of the word that represents the magnitude of the number (thousand, million, billion, etc)
Parameters:
- Number
- Number - Decimal place to round to (OPTIONAL) || Defaulted to 15
Output: String
Explanation:
- Puts a letter at the end of a number to compress it down and make it more readable (5.5K, 13.2B, 34M, etc)
Example:
local x = module.toKMBT(2938645938,3) -- x = 2.938B
local y = module.toKMBT(125) -- y = 125
local z = module.toKMBT(-123456.5,2) -- z = -123.45K
Inverse Example:
local x = module.fromKMBT('2.938B') -- x = 2938000000
local y = module.fromKMBT('125') -- y = 125
local z = module.fromKMBT('-123.45K') -- z = -123450
To Scientific
Purpose: convert the input into scientific notation
Parameters:
- Number
- The Base (OPTIONAL) || Defaulted to 10
Output: String
Explanation: If the base is set to 2 and the input is 32, then the output looks like 1 * 2^5, if the base was 10, it would output 3.2 * 10^1
- *This *
Example:
local x = module.toScientific(2938645938) -- x = 2.938645938 * 10^9
local y = module.toScientific(125,25) -- y = 5 * 25^1
local z = module.toScientific(-123456.5,5) -- z = -1.5802432 * 5^7
Inverse Example:
local x = module.fromScientific('2.938645938 * 10^9') -- x = 2938645938
local y = module.fromScientific('5 * 25^1') -- y = 125
local z = module.fromScientific('-1.5802432 * 5^7') -- z = -123450
To Numeral
Purpose: convert the input into a roman numeral
Parameters:
- Number
Output: String
Explanation:
-
Roman numerals are a bit weird, here’s my basic understanding
If you assign values to each letter (I=1, V=5, X=10…)
Most numerals are basic addition
XXXVII = 10+10+10+5+1+1 = 37
but sometimes it looks like this
XXXVXII if the smaller value is in front of a larger one you subtract them, in this case, V is in front of X, so you do X-V (10-5), and add the rest up as normal
10+10+10+(10-5)+1+1 = 37
Example:
local x = module.toNumeral(293) -- x = CCXCIII
local y = module.toNumeral(125) -- CXXV
local z = module.toNumeral(19) -- z = XIX
Inverse Example:
local x = module.fromNumeral('CCXCIII') -- x = 293
local y = module.fromNumeral('CXXV') -- y = 125
local z = module.fromNumeral('XIX') -- z = 19
To Percent
Purpose: Convert a decimal into a percentage
Parameters:
- Number
- Number - Decimal place to round to (OPTIONAL) || Defaulted to 15
Output: String
Explanation:
- Multiplies a number by 100 and puts a percent sign at the end, crazy stuff
Example:
local x = module.toPercent(.541) -- x = 54.1%
local y = module.toPercent(.141592653589,3) -- y = 14.159%
local z = module.toPercent(-.123456,2) -- z = -12.34%
Inverse Example:
local x = module.fromPercent('54.1%') -- x = .541
local y = module.fromPercent('14.159%') -- y = .14159
local z = module.fromPercent('-12.34%') -- z = -.1234
To Fraction
Purpose: Convert a number into a fraction
Parameters:
- Number
- Mixed Number Toggle (OPTIONAL) || Defaulted to false
Output: String
Explanation:
- Converts a number into its simplified fraction, the second parameter toggles the mixed number mode, if set to false it will return an improper fraction
Example:
local x = module.toFraction(3.5,true) -- x = '3 1/2'
local y = module.toFraction(1.2) -- y = '6/5'
local z = module.toFraction(.6,false) -- z = '3/5'
Inverse Example:
local x = module.fromFraction('3 1/2') -- x = 3.5
local y = module.fromFraction('6/5') -- y = 1.2
local z = module.fromFraction('3/5') -- z = .6
To Time
Purpose: Convert number into a 12/24 hour time format
Parameters:
- Number
- AM/PM Toggle (OPTIONAL) || Defaulted to false
Output: String
Explanation:
- If the 2nd parameter is true then the function will return an am/pm format, if it’s false or nil then it’ll return the 24-hour format
Example:
local x = module.toTime(3.5,false) -- x = '3:30:00'
local y = module.toTime(13.25) -- y = '13:15:00'
local z = module.toTime(12.11,true) -- z = '12:06:36 PM'
Inverse Example:
local x = module.fromTime('3:30:00') -- x = 3.5
local y = module.fromTime('13:15:00') -- y = 13.25
local z = module.fromTime('12:06:36 PM') -- z = 12.11
Prime Factorization
Purpose: Get the prime factorization of a given input
Parameters:
- Number
Output: String
Explanation:
- For example 12 has a prime factorization of 2^2×3^1, since the bases are prime and this expression equals 12
Example:
local x = module.primeFactor(144) -- x = {{3,2},{2,4}} (this is saying 3^2×2^4 = 144
local y = module.toPercent(97) -- y = {{97,1}}
local z = module.toPercent(13*11) -- z = {{13,1},{11,1}}
To Base
Purpose: Converts an integer in some base, into another base
Parameters:
- Integer/String
- Number - Base To convert the Integers to
- Number - The Integers current base
Output: String/Integer
Explanation:
-
Deep Breath
Converting Bases requires you to first convert the integer (let’s say 123456) in base (let’s say 7) to base 10
You loop through all the digits and multiply them by the base^the index minus 1
(1×7^5)+(2×7^4)+(3×7^3)+(4×7^2)+(5×7^1)+(6×7^0), which equals 22875
now we want to convert this Integer to base 16, what you do is find the remainders of Integers
22875%16 = 11 (11 in this case gets converted to B, since 9 = 9, 10 = A, 11 = B), this is the last digit
22875/16 = 1429r11
1429/16 = 89r5 (5 is the second to last digit)
89/16 = 5r9 (9 is the third to last digit)
5/16 = 0r5 (5 is the first digit, since the whole part of the quotient is 0, and the loop terminates)
and you end up with 595B, not to be confused with 595 billion)
Example:
local x = module.toBase(12345,2,16) -- x = 10010001101000101
local y = module.toBase(10010001101000101,16,2) -- y = 12344 (Lua is pretty god awful with big Integers, so it rounds 10010001101000101 to 10010001101000100, which takes 1 digit off of the final answer)
local z = module.toBase('fffff',10,16) -- z = 16777215
To Fahrenheit
Purpose: Converts celsius to fahrenheit
Parameters:
- Number
Output: Number
Explanation:
- Celsius and Fahrenheit are two units of measuring temperature, the formula for Celsius to Fahrenheit is F = 9F/5+32, and Fahrenheit to Celsius is C=5(F-32)/9
Example:
local x = module.toFahrenheit(0) -- x = 32
local y = module.toFahrenheit(100) -- y = 212
local z = module.toFahrenheit(77) -- z = 25
To Celsius
Purpose: Converts fahrenheit to celsius
Parameters:
- Number
Output: Number
Explanation:
- Celsius and Fahrenheit are two units of measuring temperature, the formula for Celsius to Fahrenheit is F = 9F/5+32, and Fahrenheit to Celsius is C=5(F-32)/9
Example:
local x = module.toCelsius(32) -- x = 0
local y = module.toCelsius(212) -- y = 100
local z = module.toCelsius(25) -- z = 77
Vertex Calculator
Purpose: Calculates the vertex of a parabola
Parameters:
- a
- b
- c
Output: Number, Number
Explanation:
-
The vertex of a parabola is the point where the rate of change is 0, where the graph is neither increasing nor decreasing
Example:
local x = module.vertex(1,13,40) -- x = -6.5,-2.25
local y = module.vertex(1,0,-36) -- y = 0,-36
local z = module.vertex(2,-3,-18) -- z = 1.5,-20.25
Solver
Purpose: Finds the zeros of any equation
Parameters:
- Function
Output: Table
Explanation:
-
Finds all x values where the function is equal to zero.
If you want the exact algorithm for this:
Newton’s method - Wikipedia
Example:
local x = module.solver(function(x) return 2^x end) -- x = {} (2^x never touches the x axis, it has an asymptote of 0)
local y = module.solver(function(x) return math.sqrt(x) - 2 end) -- y = {4}
local z = module.solver(function(x) return x^5 - 5*x + 3 end) -- z = {-1.6180339887499,0.61803398874989,1.27568220365099}
Lambert W function - Branch 0
Purpose: find the value of x for an equation in the form of x*e^x when its equal to some number
Parameters:
- Number - y
Output: Table
Explanation:
Example:
local x = module.lambert_w0(5*math.exp(5)) -- x = 5
local y = module.lambert_w0(3*math.exp(3)) -- y = 3
local z = module.lambert_w0(2) -- z = 0.8526055020137
local a = module.lambert_w0(module.Complex.i) -- a = 0.37469902073711625+0.5764127230314329i
local b = module.lambert_w0(-.25) -- b = -0.3574029561813889
Lambert W function - Branch -1
Purpose: find the value of x for an equation in the form of x*e^x when its equal to some number
Parameters:
- Number - y
Output: Table
Range: -1/e to 0
Explanation:
Example:
local x = module.lambert_wm1(5*math.exp(5)) -- x =
local y = module.lambert_wm1(3*math.exp(3)) -- y =
local z = module.lambert_wm1(2) -- z =
local a = module.lambert_wm1(module.Complex.i) -- a =
local b = module.lambert_wm1(-.25) -- b = -2.15329236411035
Tetration
Purpose: calculate x^x, a certain amount of times
Parameters:
- Number -
- Iteration Count - how many times is x taken to the xth power (OPTIONAL) || Defaulted to 2
Output: Number/Table
Explanation:
-
if you input 5,2 as the parameters, it will return 5^5, if you input 2,4, it will return 2^2^2^2.
Heres more on tetration:
Tetration - Wikipedia
Example:
local x = module.tetration(math.sqrt(2),10000) -- x = 2 -- fun fact the infinite tetration of root 2 is 2!!
local y = module.tetration(3) -- y = 3^3=27
local z = module.tetration(i,10000) -- z = 0.43828293672702395+0.3605924718713796i
Calculus
To be honest I barely understand this, very pointless functions unless taking a calculus course
Derivatives
Purpose: Calculate the instant rate of change at a given point on a function
Parameters:
- Number - The given x value
- Function
Output: Number
Explanation:
-
Basically this finds the instant rate of change at a given point (x) on function (f), if the function is decreasing at point x, its rate of change is negative, if increasing, it is positive, if it isn’t increasing or decreasing, its rate of change is 0.
Here’s another Wikipedia article if you’re really into this:
Derivative - Wikipedia
Example:
local x = module.derivative(5 , function(x) return x^2 end) -- x = 10.00088900582341 (This is supposed to be 10, but you have to have very precise numbers in order for it to give you an exact number, lua is really bad with small and big numbers)
local y = module.derivative(2 , function(x) return math.sqrt(x) end) -- y = 0.3530509218307998
Integrals
Purpose: Calculate the area under a curve from point a to b for function f
Parameters:
- Number - Lower Bound
- Number - Upper Bound
- Function
Output: Number
Explanation:
-
An integral can be described as the area under a function from two bounds, that’s about it
Wikipedia!:
Integral - Wikipedia
Example:
local x = module.integral(0, 5, function(x) return x^2 end) -- x = 41.66679166688157 (supposed to be 41.66666... lua is bad with very big and very small numbers
local y = module.integral(0, 5, function(x) return math.sqrt(x) end) -- y = 7.4535599249992989
Limits
Purpose: Find the limit where x approaches some number in f(x)
Parameters:
- Number
- Function
Output: Table
Explanation:
-
Sometimes functions have a hole in the graph,
usually meaning that when you input x, you’re dividing by 0 which can’t happen, so to fix that issue, you get the limit of the function at the point where that hole lies, more on Wikipedia:
Limit - Wikipedia
Example:
local x = module.limit(-6, function(x) return (x^2 + 12*x + 36)/(x+6) end) -- x = 0
local y = module.limit(0, function(x) return -(x^3 - 3*x)/x end) -- y = 3
Summation
Purpose: Add up a sequence of numbers
Parameters:
- Number - Start Bound
- Number - Finish Bound
- Function (OPTIONAL) || Defaulted to no function applied
Output: Table
Explanation:
-
How this works is by creating a set of consecutive integers from the start bound to the finish bound, and all these integers have been put through a function, and then adding these outputs up, basically if the parameters looked like 0 for the start bound and 10 for the finish bound, and the function applied is x^2, then you do: 0^2+1^2+2^2+3^2+4^2…+10^2. And you get 385
Wikipedia Article:
Summation - Wikipedia
Example:
local x = module.summation(1, 10) -- x = 55
local y = module.summation(0, 5, function(x) return n^2 end) -- y = 55
Product
Purpose: Multiply together a sequence of numbers
Parameters:
- Number - Start Bound
- Number - Finish Bound
- Function (OPTIONAL) || Defaulted to no function applied
Output: Table
Explanation:
-
How this works is by creating a set of consecutive integers from the start bound to the finish bound, and all these integers have been put through a function, and then multiplying these outputs together, basically, if the parameters looked like 1 for the start bound and 10 for the finish bound, and the function applied is x^2, then you do: 1^2 * 2^2 * 3^2 * 4^2… * 10^2. And you get 385
Wikipedia Article:
Multiplication - Wikipedia
Example:
local x = module.product(1, 10) -- x = 3628800
local y = module.product(1, 5, function(x) return n^2 end) -- y = 14400
Physics
Some functions to help with physics calculations (excluding air resistance). Note that all inputs of distance, velocity, and acceleration are in terms of meters and seconds. All angles are in radians.
Max Height
Purpose: Find the max height of a projectile launched at some angle and some magnitude velocity
Parameters:
- Velocity
- Angle (In radians)
Output: Number
Explanation:
- Velocity in the y direction is denoted as Vsin(θ). Solving for x (being the distance travelled in the y) using the equation Vf^2 = Vi^2 +2ax gets (Vf^2-Vi^2)/2a = x. Since at the maximum height the velocity in the y direction is 0, we can substitute 0 in for Vf (V final), Vsin(θ) in for Vi (V initial), and gravitational acceleration in for a (g, also known as -9.81m/s^2), you end up with V^2sin^2(θ)/2g, which is the formula. phew…
Example:
local x = module.maxHeight(10,math.pi/2) -- x = 5.098399102681758 (meters)
local y = module.maxHeight(25,math.pi/6) -- y = 7.966248597940243 (meters)
Travel Time
Purpose: Find the travel time (time in the air) of a projectile launched at some angle and some magnitude velocity
Parameters:
- Velocity
- Angle (In radians)
Output: Number
Explanation:
- nope, if you really want an explanation contact me!
Example:
local x = module.travelTime(10,math.pi/2) -- x = 1.0196798205363513 (seconds)
local y = module.travelTime(25,math.pi/6) -- y = 2.5491995513408785 (seconds)
Gravitational Force
Purpose: Find the Force in Netwons, of two objects with some mass, and some distance apart
Parameters:
- Mass 1
- Mass 2
- Distance from each other
Output: Number
Explanation:
- nope, if you really want an explanation contact me!
Example:
local x = module.gravitationalForce(5.97219*10^24,7.34767309 * 10^22,3.84*10^8) -- x = 198612782213422320000 (newtons) (force between earth and moon)
local y = module.gravitationalForce(5.97219*10^24,1.9891*10^301,5*10^11) -- y = inf (newtons) (not actually infinite, but too large for lua to handle)
Centripetal Force
Purpose: Find the force require to keep an object moving in a circular motion
Parameters:
- Mass of Object
- Velocity
- Radius of Circle
Output: Number
Explanation:
- Imagine a car weighing 1500kg going 5 m/s, turning on a curve with a radius of 2 meters. The force required to keep it on the road is 18750N
Example:
local x = module.centripetalForce(1500,5,2) -- x = 18750 (newtons)
local y = module.centripetalForce(1500,5,10) -- x = 3750 (newtons) (same car going around a curve that has a radius of 10
Useless
This is where I goof around adding the most pointless of the pointless functions, don’t judge me
Digits Add
Purpose: combine the digits of a number
Parameters:
- Integer
Output: Integer
Explanation:
- Adds up all the digits of the input
Example:
local x = module.digitadd(12345) -- x = 15 (1+2+3+4+5=15)
local y = module.digitadd(712369482384) -- y = 57
Digits Multiply
Purpose: multiply the digits of a number together
Parameters:
- Integer
Output: Integer
Explanation:
- Multiply up all the digits of the input
Example:
local x = module.digitmul(12345) -- x = 120 (1*2*3*4*5=120)
local y = module.digitmul(712369482384) -- y = 13934592
Digits Reverse
Purpose: reverse a numbers digits
Parameters:
- Integer
Output: Integer
Explanation:
- reverse a number (81 becomes 18, 64 becomes 46)
Example:
local x = module.digitrev(12345) -- x = 54321
local y = module.digitrev(712369482384) -- y = 483284963217
Imaginary Library
These functions assist you when working with arithmetic on complex numbers.
Note: i is a data type in the form of a table, you cant use it in ordinary math functions since it will return an error: invalid argument #1 to 'functionName' (number expected, got table)
local complexNum = 1+2*i -- This represents 1+2i
local realNum = 2 -- this represents 2+0i, this is a valid input
local imaginaryNum = 5*i -- this represents 0+5i, this is a valid input
local complexLibrary = module.Complex -- this is how you call the library
To Polar Form
Purpose: convert a rectangular value to polar
Parameters:
- Table/Number - {a,b}
- String Format Toggle (OPTIONAL) || Defaulted to false
Output: Number, Number
Explanation:
- converting a rectangular form value to polar requires you to find the distance from the origin of the imaginary axis is that point: sqrt(a^2+b^2), and the angle if there was a line to be drawn from the origin to the point is the arctan(b/a)
Example:
local
local x = complex.toPolar({2,1},true) -- x = '2.23606797749979e^0.4636476090008061i'
local distance,theta = complex.toPolar({-5,1})
-- distance = 5.0990195135927845,
-- theta = -0.19739555984988078
From Polar Form
Purpose: convert a rectangular value to polar
Parameters:
- Number - Distance
- Number - Angle
Output: Table/String
Explanation:
- Converting polar form into rectangular form requires you to convert from polar form to Euler’s identity (re^iθ = r×cos(θ) + r×isin(θ), which can just be calculated using trig functions and arithmetic
Example:
local
local x = complex.fromPolar(2.23606797749979,0.4636476090008061) -- x = '2+1i'
local y = complex.fromPolar(5.0990195135927845,0.19739555984988078) -- y = '-5,1'
To String
Purpose: convert an array to a string/number in the form of “a+bi” from the form {a,b}
Parameters:
- Table - {a,b}
Output: String/Number
Explanation:
- 1+i, which internally is represented as a table {1,1} will convert to “1+i”, 5-2i will convert to “5-2i” , i converts to “i”, this is a general idea*
Example:
local x = complex.toString(1+i) -- x = "1+i"
local y = complex.toString(5-2*i) -- y = "5-2i"
local z = complex.toString(i) -- z = "i"
To Array
Purpose: convert a string/number to an array in the form of {a,b} from the form “a+bi”
Parameters:
- String/Number
Output: String/Number
Explanation:
- “1+i” will convert to 1+i, “5-2i” will convert to 5-2i , “i” converts to i, this works sort of like tonumber, but now supports i
Example:
local x = complex.ToArray("1+i") -- x = 1+i ({1,1} internally)
local y = complex.ToArray("5-2i") -- y = 5-2i ({5,-2} internally)
local z = complex.ToArray("i") -- z = i ({0,1} internally)
To Real
Purpose: convert a complex number into its real part
Parameters:
- Number
Output: String/Number
Explanation:
- The real part of 1+i is 1, so it returns 1
Example:
local x = complex.Re(1+i) -- x = 1
local y = complex.Re(5-2*i) -- y = 5
local z = complex.Re(i) -- z = 0
To Imaginary
Purpose: convert a complex number into its imaginary part
Parameters:
- Number
Output: String/Number
Explanation:
- The imaginary part of 1+2i is 2, so it returns 2
Example:
local x = complex.Im(1+i) -- x = 1
local y = complex.Im(5-2*i) -- y = -2
local z = complex.Im(i) -- z = 1
Mandelbrot Checker
Purpose: Check if a complex number is in the mandelbrot set
Parameters:
- Table - {a,b}
- Number - Power (OPTIONAL) || Defaulted to 2
Output: Boolean
Explanation:
- This requires a bit of representation
Images
This below is the mandelbrot set
everything inside of it is a solution, so inputing any complex number inside the set will return true
What is the second parameter you ask?
Well, the mandelbrot set is generated by iterating this function an infinity amount of times
z = 0
z = z^2+c
where the z starts at 0 and c is the input. then z is equal to whatever the solution to 0^2+c is, and you repeat the process of subsituting whatever the output was back into z.
The second parameter is the power, you can tell in the equation that the set has the highest power of 2, the second parameter changes that number
Power of 3

Power of 4

Power of 5

Power of 6

With this function, you can actually generate these sets
and with a bit of modification to the function, you can get very detailed
and yes, even with different powers
How the function determines if something is in or out of the set, if checking if the real part of z to the power of 2 plus the imaginary part to the power of 2 is less than 4, if it is than its apart of the set, else, it isnt
Example:
local
local x = complex.mandelbrot({0,1},2) -- x = true
local y = complex.mandelbrot({0,1},4) -- x = false
local z = complex.mandelbrot({-2,0}) -- x = true
This library also contains many math library functions now are compatible with output and input of complex numbers, such as:
- Sine (sin)
- Cosine (cos)
- Tangent (tan)
- Arcsine (asin)
- Arccosine (acos)
- Arctangent (atan)
- Sine Hyperbolic (sinh)
- Cosine Hyperbolic (cosh)
- Tangent Hyperbolic (tanh)
- Logarithm - The base and argument can be complex and/or negative (log)
- Power (pow)
- Square Root (sqrt)
- Absolute Value (abs)
- Min (abs)
- Max (abs)
And also makes some normal functions compatible with complex numbers
- Nth Fibonacci Number (fibonacci)
- Nth Lucas Number (lucas)
- Summation/Product (summation/product)
- Vertex Calculator (vertex)
- Tetration (tetration)
- Integral (integral)
- Limit (limit)
- Derivative (derivative)
- Average (avg)
- Lambert W branch 0 (lambert_w0)
Euler's Constant
Purpose: return the number e
Output: Number
Explanation:
-
This is Euler’s constant, and here’s Wikipedia:
e (mathematical constant) - Wikipedia
Example:
local e = module.e -- e = 2.718281828459045
The Golden Ratio
Purpose: return the number phi
Output: Number
Explanation:
-
Wikipedia does a lot better job at explaining things:
Golden ratio - Wikipedia
Example:
local phi = module.phi -- phi = 1.618033988749895
Pi
Purpose: return the number pi
Output: Number
Explanation:
-
We love pi, so does Wikipedia!
Pi - Wikipedia
Example:
local pi = module.pi -- pi = 3.141592653589793
Big G
Purpose: return the number G (Gravitational Constant)
Output: Number
Explanation:
-
The universe is big and confusing
Gravitational constant
Example:
local G = module.G -- G = 6.674e-11
g
Purpose: return the number g (Earths gravitational acceleration)
Output: Number
Explanation:
-
The universe is big and confusing
Gravitational Acceleration
Example:
local g = module.g -- g = 9.807
Tau
Purpose: return the number tau
Output: Number
Explanation:
- All tau is is 2×pi
Example:
local tau = module.tau -- tau = 6.283185307179586
This may not concern anyone whos just here for the module, however, if you’ve taken notice of another module already under the name MathAddons, and to put into words, I am the same person, I’ve been terminated for unfair reasons. I won’t go into the depth of the ban, I am only trying to clear up any confusion.
This module is a complete remake of its predecessor, and contains 50 functions, while the previous one only contained 26. The previous module (obviously) won’t be receiving updates.
(Note that some functions that perform the same task, may have different parameters and/or different names, do make sure you are making the necessary changes to your code of you are switching)
If you have any issues or critiques about the module please leave a reply, I’m currently a student whos only taken the Algebra I & Geometry class (and will take Algebra II), so if I incorrectly explained anything (especially in the Calculus category), please get my attention!












 JK LOL
JK LOL