Before we start I want to say this is a port from my website and this is just optimized for the devforum. However I wrote the examples in lua and though’t it might be helpful if you’d guys knew what matricies are. Anyways here are,
Matrices
A Matrix or Matrices (plural) is a 2 dimensional array consisting of numbers. They are used to store data with rows and columns. For example this matrix has 4 columns and 4 rows.

Matrices are useful for storing data that we couldn’t normally store in a traditional variable. Suppose we wanted to create a 2 by 2 bitmap for storing information on what the player owns on their plot. 1 representing they own it and 0 representing they don’t. We can iterate through the length of our matrix, or in other words how many plots can be bought on the x and z, or rows and columns in other words. From there we can create another array storing finally the actual value. In a sense we have a number inside an array - the row it inherits and inside of all of those rows the actual matrix.
local matrix = {}
local matrixColoumnLength = 2
local matrixRowLength = 2
for row=1,matrixRowLength do
matrix[row] = {}
for coloumn=1, matrixColoumnLength do
matrix[row][coloumn] = 0
end
end
matrix[1][2] = 1
matrix[2][1] = 1
Matrices don’t just have to be bit maps. They can also be used to store variables in a more elegant manner. Suppose we have this model
local variable1 = 0
local variable2 = 0
local variable3 = 0
local variable4 = 0
local variable5 = 0
local variable6 = 0
local variable7 = 0
local variable8 = 0
local variable9 = 0
local variable10 = 0
We are saying the same thing for every variable. We can follow the DRY principle here by simply treating the index of the matrix as the name and the value as the, well default value of 0.
local matrix = {}
local matrixRowLength = 10
for row=1,matrixRowLength do
matrix[row] = 0
end
This is essentially what an array is, a one dimensional matrix. You may be wondering can three dimensional matrices exist? Well they can’t, at least with the math I am going to show you after this. What you are looking for are what we call “tensors”. In short they are an abstraction from matrices that extend to three dimensional and theoretically four dimension space too.
Adding together 2 matrices is fairly simple. We just add up each of its “components” - the individual numbers, themselves - correspondent to the index of the other matrix. Suppose we have matrices A and B where A is
and B is
When we add them we get a matrix which is
Note that when applying arithmetic to 2 matrices their sizes, or in other words the amount of values they have, have to be the same. For subtraction the process is the exact same, when subtracting A from B we get a matrix which is
We got this because we subtracted the components from matrix “A” from the components of matrix “B”. If you are familiar with vectors you will know of the term “Scalar”. It is a number we apply to the normalized vector to give it magnitude, length. In matrices we do the exact same thing. Just like with vector components when wanting to multiply a matrix by a constant we multiply all of its components by that scalar. This process is known as “Scalar Multiplication”. An example of scalar multiplication on matrices is
Similarly, getting the negative of an individual matrix involves you multiplying each component of the matrix you want to make negative by -1. That also means that if we have a negative value in our matrix it will become positive too. However we are still doing scalar multiplication to it. The only difference is that the scalar needs to be -1 though.
How about if we wanted to combine some matrices together? Doing this is a bit tricky but what we need to do in a sense is solve the dot product of their rows or columns together. What this means is that we multiply matching components of the matrices then sum up. For example suppose we have matrix C
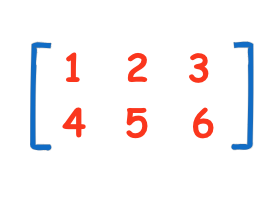
And matrix D

We get the first row of matrix C (1,2,3) and the first column of matrix D (7,9,11) . We then get the dot product by multiplying their components by each other and getting the sum of them.

That gives us 58, meaning for our new matrix the first row and column will be 58. We repeat this for all the rows and columns to get our new multiplied matrix. In this example our new matrix would be

Note that when multiplying 2 matrices together at least 1 of their rows or columns need to be equivalent in terms of amount. So a matrix with 2 columns and 1 row and another with 5 columns and 3 rows would not work. It should also be noted that the matrix does not need to be 2 dimensional for this to work either. Multiplying bit maps or identity matrices cannot have their placement changed. To add on we need to multiply like this because when attempting to multiply with the commutative law we get very different results. When reading equations of matrices note that a T in the top right hand of the matrix indicates it is being transposed. This means that you are swapping the numbers with the rows and columns.
When dividing matrices we first need to get the inverse of every component. From there we can set that as a new matrix. From there we do matrix multiplication.
To conclude, the applications for matrices can range from serialization to perhaps a grid system. The point is they store data. Matrices are commonly used in Optics, Economics, Chemistry, Geology, Animation, Finances and it is even used in wireless technologies! We can’t divide matrices or multiply like we would normally do in basic arithmetic but these are the tricks we can do to perform arithmetic and program matrices.
If you are still confused you can watch the video version here








