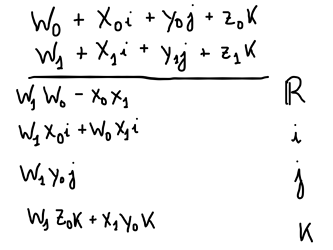Within a rotation in video games are hidden mysterious mathematics, which are not talked about.
There are different ways to rotate an object, there are Euler angles and Quaternions but, in this post, we are going to focus mainly on quaternions and why we should use them.
Required knowledge:
- Vectors.
- Radians.
- Basic trigonometry (sin and cos).
- CFrame
Euler Angles and Gimbal Lock
Normally we use this method to rotate objects because it is the most visual and simple to use, just put an angle in radians in each axis to say what rotation it has and you would have it done, but the bad thing is that it generates a problem:
To put us in situation, when using Euler angles, what we do is to convert each of the axes to a matrix:
Once this is done, the matrices are multiplied and the resulting matrix is applied. HERE IS THE PROBLEM! Matrix multiplication is not commutative, causing what is known as “Gimbal Lock”.
Gimbal Lock is the locking of an axis, causing us to lose it and when rotating the axis nothing happens:

QUATERNIONS
1. Imaginary numbers
1.1 What are imaginary numbers?
Imaginary numbers are numbers we sometimes need but do not really exist. For example, take the following equation:
x² + 1 = 0
Here we know that x has to be -1, since -1 + 1 = 0, but… How much is x worth? normally for this we use the square root, but here we are going to see a problem, and it is that the square root of a negative number does not have a real solution, since there is no number that when multiplying it by itself returns a negative number. In order to solve this, let’s “imagine” a number, the i:
√(x²) = √(-1) = i
1.2 What happens if we raise an imaginary number?
Raising an imaginary number is a somewhat curious thing since, normally, by raising one number to another we obtain a larger and larger number, but here it is not so, since:
- i = √(-1)
- i² = -1
- i³ = -i
- i⁴ = 1
- i⁵ = i
- i⁶ = -1
This list is repeated in an infinite loop.
We can see it in a more visual way with this image:
2. Complex numbers
2.1 What are complex numbers?
Complex numbers are the calculation between two numbers of different types: a + bi
By looking at a+bi, we can see the sum of two types of numbers, the a which is a real number and the bi which is an imaginary number.
a and b can be any real number, here are some examples: 5 + 3i, 34 - i, 5 - 6i, -7 + 4i…
2.2 The complex plane
The complex plane is a very similar thing to the Cartesian plane, but with one difference: the vertical axis is going to be imaginary numbers. Something like this:

As we can see, the horizontal axis becomes the integer axis, and the vertical axis becomes the imaginary axis.
This allows us to see the complex numbers proceeding in the same way as if we wanted to draw a point in the Cartesian plane:

2.3 Addition and multiplication of complexes
2.3.1 Sum of complexes
For the sum of complexes is very simple, it is like the vectors, we simply add the different axes independently, that is to say, we add the real axis with the real axis and the imaginary axis with the imaginary axis:
(a + bi) + (c + di) = ((a + c) + (b + d)i)
(5 + 2i) + (-3 - 1i) = ((5 - 3) + (2 - 1)i) = 2 + 1i = 2+i
2.3.2 Multiplication of complexes
For multiplication we do proceed in a slightly stranger way: the first step is to multiply the real component of the second complex by the real component of the first complex and by the imaginary part of the first complex:

Then, we do the same step with the imaginary component of the second complex:

Now some of you may find it strange that there are two imaginary components here, but if you look closely it is not true. We can see that we get i² there, but we know that i² = -1, so we multiply 10 by -1, leaving an integer:

Now we have another 2 complexes, which we must add:

Ready! We now have the solution to this multiplication. As you can appreciate it is a little strange the multiplication of complexes, but it is still simple, you just have to remember the steps.
3. Where do imaginary and complex numbers come from?
To demonstrate what we have seen so far and to improve our understanding of these concepts, let’s look at a complex number as two numbers:
z = (a, b); z ∈ ℂ
Now let’s define addition and multiplication:
(a, b) + (c, d) = (a + c, b + d)
(a, b) * (c, d) = (ac - bd, ad + bc)
With this we can now prove that (x, 0) = x:
(a, 0) + (b, 0) = (a + b, 0 + 0) = (a + b, 0)
(a, 0) * (b, 0) = (ab - 0, 0 + 0) ) = (ab, 0)
(x, 0) = x
Perfect! We already have the first demonstration, now let’s define i as follows:
i = (0, 1)
With this, let’s see what happens if we multiply i by some number:
bi = (b, 0) * (0, 1) = (0, b)
Once this has been demonstrated, we can rewrite a complex number as:
(a, b) = (a, 0) + (0, b) = a + bi
Here we have the form of the complex numbers demonstrated! With this we can also show what happens when we raise the imaginary numbers:
i² = (0, 1) * (0, 1) = (-1, 0) = -1
i³ = (0, 1) * (0, 1) * (0, 1) = (0, -1) = -i
i⁴ = (0, 1) * (0, 1) * (0, 1) * (0, 1) = (1, 0) = 1
And since we know that i² is -1, we already know that i must be worth √(-1).
4. More imaginary numbers in the space
In the world of imaginary numbers, there is not only the i, we also have more imaginary numbers, such as the j or the k.
These can be seen as axes in the complex plane, i being the X-axis, j the Y-axis and k the Z-axis:
i = <1, 0, 0>
j = <0, 1, 0>
k = <0, 0, 1>

Here we have something curious, and that is that the product of these is not commutative. Doing the calculation we can see the following rule:
ij = k
ji = -k
jk = i
kj = -i
ki = j
ik = -j
This is easy to check, the calculation is the same as Cross Product.
When we are working with these imaginaries, we also have the following property:
i² = j² = k² = ijk = -1
5. Quaternions
5.1 What are quaternions?
A quaternion is a complex number with 4 numbers (one real and the other 3 imaginary) with the following identity:
a + bi + cj + dk
The quaternions, as we can see, have 4 dimensions, the W corresponding to the real component, the X corresponding to the i, the Y corresponding to the j, and the Z corresponding to the k.
We can see that Roblox offers in its CFrame library a function to use quaternions:
CFrame.new(x, y, z, qX, qY, qZ, qW)
The x, y, z being the position and the qX, qY, qZ and qW being the axes of the quaternion.
This is useful to rotate in a 3-dimensional space preventing Gimbal Lock.
5.2 Rotating on an axis with quaternions
To rotate on a single axis with quaternions we proceed as follows:
Because this is a complex number (which can be viewed as a point in the complex plane), we must pass to the quaternion a position from an angle. If we know trigonometry, we know that we do this using some basic trigonometry:
cos(θ), sin(θ)
But here we have a problem, when we work with quaternions we have a double rotation, so the angle must be divided by 2:
cos(θ/2), sin(θ/2)
The cosine will be placed on the W axis and the sine on the axis we want to rotate our quaternion.
In the following script, we will see a 45º rotation on the X axis with quaternions:
local object = script.Parent
local position = object.Position
local angle = math.pi/4
angle *= .5
local quaternion = CFrame.new(position.X, position.Y, position.Z, --> Position
math.sin(angle), 0, 0, math.cos(angle) --> Quaternion
)
object.CFrame = quaternion

5.3 Multiplying quaternions
The multiplication of quaternions is an odyssey. Since we know that a quaternion is a complex number in the end, we proceed in the same way as with a + bi: multiply all the ones below with all the ones above.
Let’s make an example: to tidy up a bit, let’s do the following:
What I put on the right is to know where to put things: if I get a real number, I put it with the reals, if I get the imaginary “i”, I put it with the imaginary “i” and so on.
Let’s start with the W of the second quaternion, what we do is to multiply it with all the axes of the first quaternion respecting the rule I mentioned before:
The w is the easiest, but with the first imaginary axis it gets a little complicated. For the greatest possible understanding, I will go step by step:
First we multiply the x with the w, giving us as a result an imaginary number belonging to the “i”, thus giving us:
Then we have to multiply both x, which have an imaginary number “i”, thus giving us a negative integer, since i² = -1:
Perfect, it’s not long now! Now we multiply by the y-axis, which gives us an imaginary “j” that multiplies by i, ij = k, so it gives us positive in the k part:
And we only have to multiply by the z, which gives us an imaginary k, ik = -j, for which it gives us a negative and we must put it with the j:
If we continue with this process until the end, we will be left with the following formula:
(w₀w₁ - x₀x₁ - y₀y₁ -z₀z₁) +
(w₁x₀ + w₀x₁ + y₁z₀ - z₁y₀) i +
(w₁y₀ - x₁z₀ + w₀y₁ + z₁x₀) j +
(w₁z₀ + x₁y₀ - y₁x₀ + w₀z₁) k
Visualize in code.
local angle0, angle1 = math.pi/4, math.pi/4
angle0 *= .5
angle1 *= .5
local quaternion0 = {W = math.cos(angle0), X = 0, Y = math.sin(angle0), Z = 0}
local quaternion1 = {W = math.cos(angle1), X = math.sin(angle1), Y = 0, Z = 0}
local function multiply(q0, q1)
return {
W = q1.W * q0.W - q1.X * q0.X - q1.Y * q0.Y - q1.Z * q0.Z;
X = q1.W * q0.X + q0.W * q1.X + q1.Y * q0.Z - q1.Z * q0.Y;
Y = q1.W * q0.Y - q1.X * q0.Z + q0.W * q1.Y + q1.Z * q0.X;
Z = q1.W * q0.Z + q1.X * q0.Y - q1.Y * q0.X + q1.Z * q0.W;
}
end
local quaternionResult = multiply(quaternion0, quaternion1)
local position = script.Parent.Position
script.Parent.CFrame = CFrame.new(position.X, position.Y, position.Z,
quaternionResult.X, quaternionResult.Y, quaternionResult.Z, quaternionResult.W
)

5.3 Identity
If we want to obtain a quaternion without any rotation, the first thing we think of is to put in all its axis 0, but remember that the W is the cosine of the angle of rotation, and the cosine of 0 is 1, so if we want to create a quaternion without rotation would be to put in the W a 1, otherwise, we will see that the object we want to rotate will disappear:
identity = 1 + 0i + 0j + 0k
CFrame.new(x, y, z, 0, 0, 0, 1)
{W = 1, X = 0, Y = 0, Z = 0}
That was it! Obviously there are more things I didn’t explain here, but we’ll leave it at that for now.
So as a little tip, I recommend you to create your own library of quaternions with OOP for the easiest use of them because, if you don’t, it can be a bit tedious to use them.