Hello roblox math lovers !!
Today I am gonna talk about the ear clipping algorithm that can be used to triangulate a polygon. This can be useful in case you want to make a irregular polygon; with that algorithm you can only have to give the vertices of the polygon and it will be filled automatically !
Before showing how to code the algorithm I would like to explain some important math concepts that are needed. So, let’s get into it.
What are you gonna learn in this tutorial ?
- Some basic stuff about the vectors
- What is the cross product and how it works
- Polygon triangulating with the ear clipping algorithm
So, what is a vector ?
It would be finicky start talking about calculus with vectors without explaining some basic stuff about them.
A vector is a mathematical entity which is represented by a straight line and an arrow indicating the way.

In order to create a vector you need two points like in the example where there is the point O (0,0) and the point A (2,3). Therefore you have to subtract to the X component of A, the X component of O, and then the same for the Y component → (2 - 0, 3 - 0) = (2,3)
Now, that you know how to create a vector, let’s talk about the module. The module of a vector is the distance between the two points. It can be calculated by doing the square root of the addition of the vector components squared → √(x^2 + y^2) or translated in roblox code:
local vector = Vector2.new(2,3)
print(math.sqrt((vector.X^2) + (vector.Y^2)))
print(vector.Magnitude) -- using .Magnitude will output the same as doing the method explained above
The module can be represented with | the name of the vector | → | OA |
Let’s start doing more complicated calculus with vectors
Before explaining what is the ear clipping and how to code it I need to talk about the cross product. The cross product is a way to multiply two vectors and the result will be a new vector in the third dimension. Yes, now we are talking about 3D vectors but don’t get scare, it is very easy to understand if you pay attention.
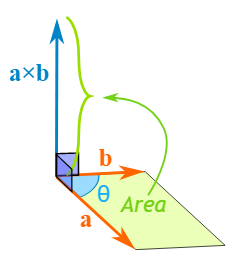
The module of the vector resulted is equal to the area of the parallelogram made by the two vectors
The formula for the cross product is the following: a × b = | a | | b | sin(θ). Let’s see what this mean: a and b are two vectors, | a | and | b | are they respective module, sin is a trigonometric formula and θ represents any angle.
We can also get the new vector using this easier way:
- c.X = a.Y x b.Z − a.Z x b.Y – the component x of the new vector
- c.Y = a.Z x b.X − a.X x b.Z – the component y of the new vector
- c.Z = a.X x b.Y − a.Y x b.X – the component z of the new vector
You can check this link where you can see more graphically how the cross product works.
What the hell is the ear clipping ?
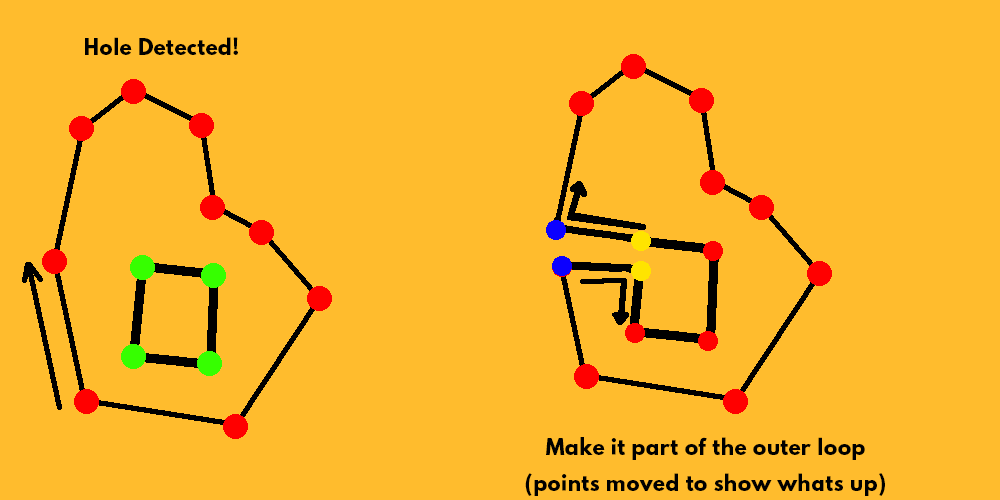
A lot of people have never heard about the ear clipping, and I don’t gonna lie, a week ago, me neither. The ear clipping method is one of the methods for triangulating polygons, it is not the fastest but it is easy to implement on code so I decided to do it. (Something important to say is that this algorithm doesn’t work with polygons that have holes).
This triangulating method is based on the Two Ears Theorem which says that any polygon with more than 3 vertices will have to ears/triangles. The ear clipping consists on finding one ear and removing it from the polygon ( this results onto a new polygon ) and repeat the process until there is only one triangle left.
And, how we can find the ear ?
Easy, first we need to find a vertex and make a triangle joining the next vertex with the previous:
Then we need to check the angle “θ”. Here is where the cross product comes into play. Before making the calculus we need to define the vectors and calculate their own module:
-- Is important to call A the vector that is made with the vertex and his previous one
local vectorA = Vector2.new(a.Position.X - b.Position.X, a.Position.Z - b.Position.Z)
local vectorB = Vector2.new(a.Position.X - c.Position.X, a.Position.Z - c.Position.Z)
local moduleA = math.sqrt((vectorA.X)^2+(vectorA.Y)^2)
local moduleB = math.sqrt((vectorB.X)^2+(vectorB.Y)^2)
Just after I calculate only the Y component of the cross vector cause the other two will be zero.
-- c.Y = a.X x b.Z − a.Z x b.X
local CrossProductY = (vectorA.X * vectorB.Y) - (vectorA.Y * vectorB.X)
( here you can see that in the comment I put b.Z and a.Z and then in the variable I put .Y, that’s because in the Vector2 the Y component is the same as the Z component in Vector3 )
So, now that we have calculated the cross product of the two vectors we can get the angle and check if is lower to 180 degrees ( if is higher it’s impossible to make a triangle!)
-- a × b = |a| |b| sin(θ)
-- sin(θ) = (a x b)/(|a| |b|)
local sin = CrossProductY/(moduleA*moduleB)
local angle = math.deg(math.asin(sin)) -- math.asin let's you get the angle of a given sin
Now that we have checked we can make a triangle we have to check if there is any other vertex inside the triangle. For that I used the cross product as well. Let me show you how I did it.
First, I make a vector from to point to every vertex of the triangle. Then, I check the direction of the angle ( I make the direction from one vector to the next using the shortest angle ). If all the directions go in the same way means that the point is into the triangle as we can se in the image, if not, we can verify that the point is out.
For that, I make the cross product of every vector with the next one and check if it is positive or negative:
function checkPointIntoTriangle(point: Instance, a: Instance, b:Instance, c:Instance)
local pointToa = Vector2.new(point.Position.X - a.Position.X, point.Position.Z - a.Position.Z)
local pointTob = Vector2.new(point.Position.X - b.Position.X, point.Position.Z - b.Position.Z)
local pointToc = Vector2.new(point.Position.X - c.Position.X, point.Position.Z - c.Position.Z)
local moduleA = math.sqrt((pointToa.X)^2+(pointToa.Y)^2)
local moduleB = math.sqrt((pointTob.X)^2+(pointTob.Y)^2)
local moduleC = math.sqrt((pointToc.X)^2+(pointToc.Y)^2)
-- cy = axbz − azbx
local CrossProductY_1 = (pointToa.X * pointTob.Y) - (pointToa.Y * pointTob.X)
local CrossProductY_2 = (pointTob.X * pointToc.Y) - (pointTob.Y * pointToc.X)
local CrossProductY_3 = (pointToc.X * pointToa.Y) - (pointToc.Y * pointToa.X)
if CrossProductY_1 <0 or CrossProductY_2 <0 or CrossProductY_3 <0 then
return true
end
end
Finally, when I get all the triangles I draw it using a function created by the user EgoMoose
Postscript: I made a folder with all the vertices before making the script. I recommend you to make the same an call it as the same way I did, unless it wont work

Here is the complete script:
local vertices = game.Workspace:WaitForChild("Vertices")
local vertexlist = vertices:GetChildren()
local vertexfound = false
local wedge = Instance.new("WedgePart");
wedge.Anchored = true;
wedge.TopSurface = Enum.SurfaceType.Smooth;
wedge.BottomSurface = Enum.SurfaceType.Smooth;
function checkPointIntoTriangle(point: Instance, a: Instance, b:Instance, c:Instance)
local pointToa = Vector2.new(point.Position.X - a.Position.X, point.Position.Z - a.Position.Z)
local pointTob = Vector2.new(point.Position.X - b.Position.X, point.Position.Z - b.Position.Z)
local pointToc = Vector2.new(point.Position.X - c.Position.X, point.Position.Z - c.Position.Z)
local moduleA = math.sqrt((pointToa.X)^2+(pointToa.Y)^2)
local moduleB = math.sqrt((pointTob.X)^2+(pointTob.Y)^2)
local moduleC = math.sqrt((pointToc.X)^2+(pointToc.Y)^2)
-- cy = axbz − azbx
local CrossProductY_1 = (pointToa.X * pointTob.Y) - (pointToa.Y * pointTob.X)
local CrossProductY_2 = (pointTob.X * pointToc.Y) - (pointTob.Y * pointToc.X)
local CrossProductY_3 = (pointToc.X * pointToa.Y) - (pointToc.Y * pointToa.X)
if CrossProductY_1 <0 or CrossProductY_2 <0 or CrossProductY_3 <0 then
return true
end
end
function checkVertex(a: Instance,b: Instance, c:Instance)
local canMakeTriangle = true
local vectorA = Vector2.new(a.Position.X - b.Position.X, a.Position.Z - b.Position.Z)
local vectorB = Vector2.new(a.Position.X - c.Position.X, a.Position.Z - c.Position.Z)
local moduleA = math.sqrt((vectorA.X)^2+(vectorA.Y)^2)
local moduleB = math.sqrt((vectorB.X)^2+(vectorB.Y)^2)
-- cy = axbz − azbx
local CrossProductY = (vectorA.X * vectorB.Y) - (vectorA.Y * vectorB.X)
-- a × b = |a| |b| sin(θ)
-- sin(θ) = (a x b)/(|a| |b|)
local sin = CrossProductY/(moduleA*moduleB)
local angle = math.deg(math.asin(sin))
if angle > 0 then -- if the angle is higher than 180 degrees the variable angle will be a number under of 0 because the cross product will be negative
for i, v in pairs(vertexlist) do
if v ~= a and v ~= b and v ~= c then
if not checkPointIntoTriangle(v, a, b, c) then
canMakeTriangle = false
end
end
end
if canMakeTriangle then
return true
end
end
end
local function draw3dTriangle(a, b, c, parent, w1, w2)
local ab, ac, bc = b - a, c - a, c - b;
local abd, acd, bcd = ab:Dot(ab), ac:Dot(ac), bc:Dot(bc);
if (abd > acd and abd > bcd) then
c, a = a, c;
elseif (acd > bcd and acd > abd) then
a, b = b, a;
end
ab, ac, bc = b - a, c - a, c - b;
local right = ac:Cross(ab).unit;
local up = bc:Cross(right).unit;
local back = bc.unit;
local height = math.abs(ab:Dot(up));
w1 = w1 or wedge:Clone();
w1.Size = Vector3.new(0, height, math.abs(ab:Dot(back)));
w1.CFrame = CFrame.fromMatrix((a + b)/2, right, up, back);
w1.Parent = parent;
w1.BrickColor = BrickColor.random()
w2 = w2 or wedge:Clone();
w2.Size = Vector3.new(0, height, math.abs(ac:Dot(back)));
w2.CFrame = CFrame.fromMatrix((a + c)/2, -right, up, -back);
w2.Parent = parent;
w2.BrickColor = w1.BrickColor
return w1, w2;
end
while task.wait() do
for i,v in pairs(vertexlist) do
if i == 1 then
if checkVertex(v , vertexlist[i+1] , vertexlist[#vertexlist]) then
vertexfound = true
draw3dTriangle(v.Position, vertexlist[i+1].Position, vertexlist[#vertexlist].Position, workspace)
print(v.Name..","..vertexlist[i+1].Name..","..vertexlist[#vertexlist].Name)
table.remove(vertexlist, i)
end
elseif i == #vertexlist then
if checkVertex(v, vertexlist[1], vertexlist[i-1]) then
vertexfound = true
draw3dTriangle(v.Position, vertexlist[1].Position, vertexlist[i-1].Position, workspace)
print(v.Name..","..vertexlist[1].Name..","..vertexlist[i-1].Name)
table.remove(vertexlist, i)
end
elseif i ~= 1 and i ~= #vertexlist then
if checkVertex(v , vertexlist[i+1] , vertexlist[i-1]) then
vertexfound = true
draw3dTriangle(v.Position, vertexlist[i+1].Position, vertexlist[i-1].Position, workspace)
print(v.Name..","..vertexlist[1].Name..","..vertexlist[i-1].Name)
table.remove(vertexlist, i)
end
end
if vertexfound then
vertexfound = false
break
end
end
if #vertexlist <= 1 then
break
end
end
If you want to copy the original place you can !!
Thanks for taking your time to reading this tutorial and I would like to express special thanks to @Kriko_YT that told me about the ear clipping.
If you enjoyed the tutorial please consider to leave a like and comment what other math things you want to learn.