What is :Dot function do?

Help and Feedback Scripting Support
#1

Can someone tell me what this function does in dummy terms for me to understand?

2 Likes
Check if a player has looked away from a part
#2

You can check this out

6 Likes
#3

What I can tell what dot does is add up the distance between them or something like that?

#4

All Dot does is see how much 2 vectors go in the same direction. So you can compare them

#5

If you are using look vectors, I think it means how different two parts front direction is from -1-1

edit: -1 would be facing opposite directions, 0 being right angle to eachother and 1 being same direction

#6

I had (lookvect1x10):Dot(lookvect2x10) and I was getting 100 while they both faced the same direction. Shouldn’t it be 10? Is it doing multiplication or addition?

the x’s are multiplication btw.

#7

You probably want to use the Vector3’s units (Vector3.Unit) to constrain it between -1 and 1.
Example:

local V1 = Vector3.new(-10,-50,-200)
local V2 = Vector3.new(10,50,200)

print(V1.Unit:Dot(V2.Unit)) -- Returns -1
#8

What is a unit? Sorry im not very experienced.

#9

The dot product is a mathematical function that takes two vector3’s.

It returns a value between -1 and 1

This will tell you if they are facing in the same direction.

If it returns 1 that means the two vectors are pointing in the same direction
If it returns -1 they are facing in the opposite direction.

#10

Sorry for the late response, a Vector’s unit is a normalized copy of it. For example:

Vector3.new(30,50,70).Unit

would be about Vector3.new(0.329, 0.548 0.768). It’s basically a vector, but constrained between -1 and 1

1 Like
#11

The dot product is equal to the product of the magnitude of the vectors times the cosine of the angle between them.
It is equal to 0 if the vectors are perpendicular.

1 Like
#12

Vector3:Dot(Vector3) returns the dot product of the two vectors. Algebraically, it is defined as:
lagrida_latex_editor

Which we will refer to as the projection definition, where:

  • a and b are vectors involved in the operation
  • |a| and |b| represents the magnitude of vectors a and b respectively
  • Theta (greek letter) represents the angle between the two vectors

It is also worth noting that the dot product isn’t necessarily constrained to the interval [-1, 1]. This is the case if the vectors are unit vectors

It is also defined as this, which is a more useful definition as the one above as you may not always have the angle between the two vectors. It is derived using the law of cosines involving the above formula. This we will refer to as the vector component definition:
lagrida_latex_editor (1)

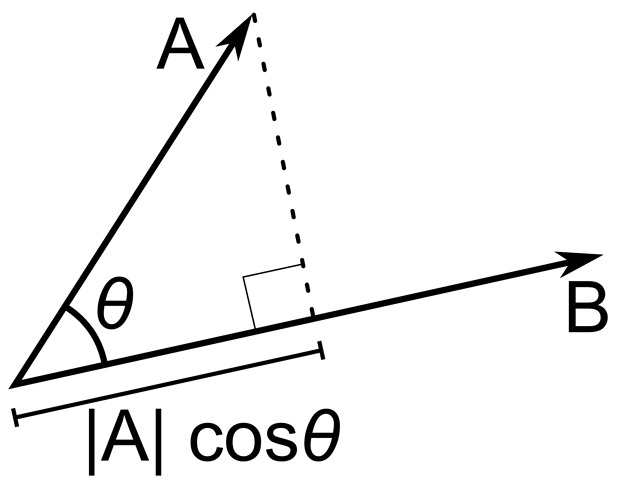
The dot product may also be defined as the scalar projection of one vector onto another multiplied by the other’s magnitude. How we get the scalar projection is by multiplying the vector’s magnitude by the cosine of the angle between them

image
image1280Ă—1024 46 KB

|A| * cos(theta) represents the scalar projection of vector A onto vector B.

The dot product has many useful applications in computer graphics, such as:

  • Determining the angle between the two vectors: Given the projection definition we had, we can transpose the equation to make theta the subject of the formula, which represents the angle between the two vectors.
    lagrida_latex_editor (2)
    This doesn’t return our angle, but it returns the cosine of the angle between the vectors. If we want the angle, we need to take the inverse cosine (or arc cosine) of this:
    image
    If the vectors are both in the same direction, then the angle will be 0 degrees/radians. In this case, our dot product is 1. If the vectors are facing completely opposite directions, then the angle will be 180 degrees, or Pi radians. The dot product will be -1 in this case. Now we have our angle. We can also put this into code:
local a = Vector3.new(10, 10, 10)
local b = -a
print(math.acos(a:Dot(b) / (a.Magnitude * b.Magnitude)))
-- above returns ~3.14 (Pi) radians. You can convert this to degrees using math.deg

  • Determining if the vectors are perpendicular: You may notice that the cosine function is involved here. When the vectors are perpendicular (i.e: 90 degrees, Pi/2 radians apart), the cosine of the angle is 0, which ultimately makes the dot product 0 since anything multiplied by 0 is 0. If our dot product is 0, the vectors are perpendicular

  • A more practical use - Reflecting a vector (based on a surface normal): You can dive into resources online, even here on the devforum to learn more about this. A surface normal in this case is a vector that is perpendicular to a surface. Commonly, raycasting is involved here so research this if you’re interested

8 Likes