What is a perceptron?
A perceptron is the simplest neural network, that consists of a single neuron, a n number of inputs and one output.
The process of passing the data through the perceptron is called forward propagation. There are three steps when the forward propagation is carried out in a perceptron.
Step 1
We multiple each input (let’s say x1) with its corresponding weight (the w1) and sum all the multiplied values.
![]()
Which can also be written as :

Step 2
Add the bias to the summation of the multiplied values . You can call this however you like, lets call it z.

Step 3
Pass the value of z to an activation function . Some popular activation functions are the following:
If you want to learn more about them or why we need them see this
What we are going to use is the sigmoid function, which as you can see from the table above is a non linear one.

Where y is the output we get after the forward propagation , σ denotes the sigmoid activation function and e is the exponential function
The Learning Process
The learning process consists of two parts , backpropagation and optimization.
Backpropagation is an algorithm used to train the neural network of the chain rule method . In simple terms, after the data passes through the perceptron (forward propagation) , this algorithm does the backward pass to adjust the model’s parameters based on weights and biases.
The backpropagation in a perceptron is carried out in two steps
Step 1
In order to find how far we are from our desired target goal we use a loss function.

where y is the actual value and ydot is the predicted value. We calculate the loss function for the entire training dataset and their average is called the Cost function C .

Step 2
To find the best weight and bias for our perceptron it is essential to find how the cost function changes with regard to weights and the bias. The gradient of cost function C with respect to the weight wi can be calculated using the chain rule.
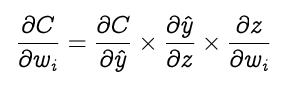
where ŷ is the predicted value, w the weight
I won’t explain the math here, you can see them here but our result with respect to the weight wi is :


and with respect to the bias this:


Optimization is the selection of the best element from some set of available alternatives, in our case, the selection of best weights and bias of the perceptron. We can choose gradient descent as our optimization algorithm, which changes the weights and bias , proportional to the negative of the gradient of the cost function with respect to the corresponding weight or bias. Learning rate ( α ) is a hyperparameter which is used to control how much the weights and bias are changed.
The weights and bias are updated as follows:

Code example
local Perceptron = {}
Perceptron.__index = Perceptron
local function sigmoid(x)
return 1/(1+ 2.71828182846 ^ x)
end
function Perceptron.new(numInputs)
local cell = {}
setmetatable(cell, Perceptron)
cell.weights = {}
cell.bias = math.random()
cell.output = 0
for i = 1, numInputs do
cell.weights[i] = math.random()
end
return cell
end
--used in both training and testing, calculates the output from inputs and weights
function Perceptron:update(inputs)
local sum = self.bias
for i = 1, #inputs do
sum = sum + self.weights[i] * inputs[i]
end
self.output = sigmoid(sum)
end
--returns the output from a given table of inputs
function Perceptron:test(inputs)
self:update(inputs)
return self.output
end
--used in training to adjust the weights and bias
function Perceptron:optimize(stepSize)
local gradient = self.delta * self.output
for i = 1, #self.weights do
self.weights[i] = self.weights[i] + (stepSize*gradient)
end
self.bias = self.bias + (stepSize*self.delta)
end
--takes a table of training data, the number of iterations (or epochs) to train over, and the step size for training
function Perceptron:train(data, iterations, stepSize)
for i = 1, iterations do
for j = 1, #data do
local datum = data[j]
self:update(datum[1])
self.delta = datum[2] - self.output
self:optimize(stepSize)
end
end
end
local node = Perceptron.new(1) --creates a new Perceptron that takes in 1 input
local trainingData = {} --this Perceptron will be trained on the sigmoid function
print("Untrained results:")
for i = -2, 2, 1 do
print(i..":", node:test({i}))
trainingData[i+3] = {{i},2*i+1} --the training data is a table, where each element is another table that has a table of inputs and one output
end
node:train(trainingData, 100, .1) --trains on the set for 100 epochs with a step size of 0.1
print("\nTrained results:")
for i = -2, 2, 1 do
print(i..":", node:test({i}))
end

