Introduction
Lua has a default math library, simply the class “math”. However I felt that some of the stuff I wanted and I am sure you too were missing from it. So I decided to make a math module, called Math++ to help us.
Installation
To install Math++ simply get a copy from it here.
https://www.roblox.com/library/5901655059/Math
You then need to place the Math++ module in a directory in which the script you will use to call the library can access. For access from the server and client I’d suggest using the ReplicatedStorage. From there simply call the require() function to a variable where the parameter of the require function is the directory path to get there, so say we have Math++ here

We can get access to it by putting the following code in the instance named “Script”
local mathLib = require(script.Parent["Math++"])
Documentation
constant: phi
Returns 1.6180339887. It is the golden ratio.print(mathLib.phi) --Output: 1.6180339887
constant: e
Returns 2.718281828459. It is Eulers Number, the base of the natural logarithm.print(mathLib.e) --Output: 2.718281828459
constant: G
Returns 6.673*10^-11. It is the gravitational constant, fundamental in modeling accurate orbital physics.print(mathLib.G) --Output: 6.673e-11
function: naturalLog(log)
Equivalent to doing math.log(e, log). This is the fundamental of exponential growth.print(mathLib.naturalLog(2)) --Output: 0.69314718055996
function: bound(min, max, value)
In a sense this maps an integer to a number from 0 to 1 between a range. So say we had our min as 0 and our max as 10 and our value was 5 we would return 0.5.print(mathLib.bound(0,10,5)) --Output: 0.5
function: derivative(x, dx, fx)
Finds the derivative of the passed function (fx) at point x. The closer dx is to 0 the more close it is to the true answer.print(mathLib.derivative(2,0.000001, function(x) return x^2 end)) --Output: 4.000001000648
function: ellipse(minorAxisLength, majorAxisLength, alpha)
Returns an array where the first element is X and the second is Y (can be replaced with Z) of a given ellipse. Contrary to the name you can still draw circles with this, the minorAxisLength just has to be equal to the majorAxisLengthfor i=0,1,0.01 do local part = Instance.new("Part") part.Position = Vector3.new(mathLib.ellipse(5,5,i)[1], 5, mathLib.ellipse(5,5,i)[2]) part.Anchored = true part.Size = Vector3.new(1,1,1) part.Parent = workspace end

function: sigmoid(z)
Maps a value to a value from 0 to 1. Similar to bound(min, max, value), the Sigmoid function maps to ± ∞. Note though, that just like the hyperbolic tangent of x this function becomes obsolete for numbers not near 0.print(mathLib.sigmoid(6.9)) --Output: 0.00100677082009
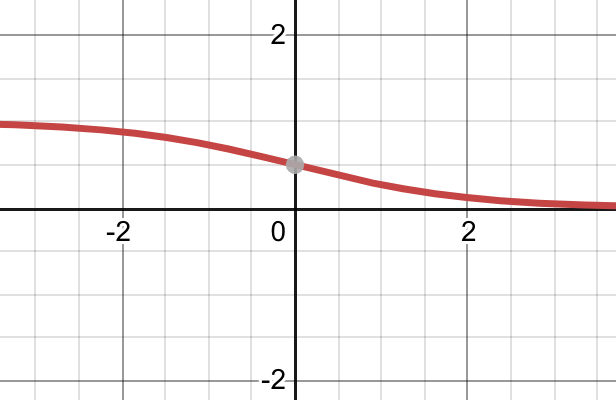
function: quadratic(a, b, c, t)
Returns a quadratic graph where t is the timestep and a is basically how spacey it is in a sense. The smaller a is the wider the trajectory. “b” correlates to how high the graph will go and c refers to the position of where the trajectory starts (relative to axis)for i=0,6,0.01 do local part = Instance.new("Part") part.Position = Vector3.new(i, mathLib.quadratic(-0.5, 3, 0, i), 0) part.Anchored = true part.Size = Vector3.new(0.1,0.1,0.1) part.Parent = workspace end

function: integral(a, b, dx, func)
Returns the definite integral from a to b. The smaller dx is to 0 the more accurate the answer is. func refers to our graph function. For further information on what a definite integral is.print(mathLib.integral(0, 1, 0.0001, function(x) return x^3 end)) --Output: 0.25005000249993
function: sum(a, b, func)
Given starting point a and end point b it gets the sum of all values from a function. Returning x on the function will be the equivalent of just doing 1+2+3 if a is 1 and b is 3.print(mathLib.sum(1, 10, function(x) return x+x end)) --Output: 110
function: prod(a, b, func)
Exact same as sum(a, b, func) except instead of returning the sum of them it is the product. Returning x will be the equivalent of doing b! if a is 1. However this won’t work if it is a non-integer. You would need to use a gamma function. Do note that just cause of how exponential prod is if you get 0 or -NaN it’s probably because the range is too large.print(mathLib.prod(1, 3, function(x) return x^2 end)) --Output: 36
function: lerp(a, b, z)
Linear interpolates a real number where z is the alpha. NOT a class. A refers to the minimum value and b refers to the maximum.print(mathLib.lerp(1, 3, 0.5)) --Output: 2
function: quadBezier(timeStep, control1, control2, control3)
Generates a bezier path from 0 to 1 (timeStep). The controls do not have to be a vector2 or a vector3.print(mathLib.quadBezier(0.5, Vector3.new(0,1,0), Vector3.new(1,0,0), Vector3.new(0,0,1))) --Output: (0.5, 0.25, 0.25) (Vector3)
function: cubicBezier(timeStep, control1, control2, control3, control4)
Same thing as quadBezier(timeStep, control1, control2, control3) but there is another control point. For a more in-depth guide on Beziers see my video here.print(mathLib.cubicBezier(0.69, Vector3.new(0,1,0), Vector3.new(1,0,0), Vector3.new(0,0,1), Vector3.new(0,1,1))) --Output: (0.731073022, 0.3583, 0.328509003 ) (Vector3)
function: eucDist(a, b, state)
Equivalent to (a.Position - b.Position).Magnitude. If you are using Vector2’s you need to pass 2 to the state parameter while for Vector3’s it is 3.print(mathLib.eucDist(workspace.A.Position, workspace.B.Position, 3)) --Output: 22.137750904447
function: manHatDist(a, b, state)
Useful in Artificial Intelligence development. This returns the distance between two points in manhattan distance.print(mathLib.manHatDist(workspace.A.Position, workspace.B.Position, 3)) --Output: 26.760003268719
function: chebDist(a, b, state)
Chebyshev distance essentially solves the chess problem. Of course it will be useful for that but it is also used in some sudoku algorithms. Note, even though it is used in the example it is encouraged you use this for 2d cartesian coordinates in euclidean space only.print(mathLib.chebDist(workspace.A.Position, workspace.B.Position, 3)) --Output: 21.504999160767
function: mat4x4(components)
this method is deprecated. Use this instead, Mat4x4 Library For Computer Graphics
Generates a 4x4 array matrix given a 1 dimensional list of 16 matrix components.local matrix = mathLib.mat4x4({1,2,3,4,1,2,3,4,1,2,3,4,1,2,3,4}) print(matrix)
function: reflect(normal, direction)
“Flips” a vector across another in a sense. Combining this with parametric ray equations you can get some cool stuff.local mathLib = require(script["Math++"]) game:GetService("RunService").Heartbeat:Connect(function() local dir = workspace.Head.Position - workspace.Tail.Position local newDir = mathLib.reflect(Vector3.new(0,1,0), dir) local p = workspace.Head.Position + newDir workspace.Aligner.CFrame = CFrame.new((p + workspace.Head.Position) / 2, p) workspace.Aligner.Size = Vector3.new(0.5, 0.5, (p-workspace.Head.Position).magnitude) workspace.AlignerO.CFrame = CFrame.new((workspace.Tail.Position + >workspace.Head.Position) / 2, workspace.Tail.Position) workspace.AlignerO.Size = Vector3.new(0.5, 0.5, (workspace.Tail.Position->workspace.Head.Position).magnitude) end)
Fun fact, this math was used in my ray tracer!



