Well, for weeks, i’ve been trying to understand Cleversource algorithm and that also includes contacting Cleversource himself ( he doesn’t response to me) but so far, i still can’t get it, i’m still quite confused about the way he calculated the angle to spin around the yaw axis. I have explained quite clear about my question in this topic(I don't understand why the Y component represent the angle between two vectors), Please check it out, i’m kind of desperate so hope that if i post on this time rather than night in my country, it will get some responses.
(((HeadPosition - Point).Unit):Cross(TorsoLookVector)).Y * 1
is dis da code u need explaination?
yeah, it is. You’re right and i;m sorry for the late response, i have to clean my pet’s cage
Hello, i was wondering if you’re there?
srry for long response.
but from here, i see its kind of to smooth da angle, lik, u can in his vid, da head wont directly look up to mouse point, but somewhere below, dis is bc of da :Cross() func.
tell me if im stoopeed and got thigs wrong, i will only be taught about 3d stuff next 2 years 
i cant represent thigs in images here, unfortunately
?,its kind of to smooth da angle
Yeah, but how does it function? Cna you pls explain it a little bit clearer?
ok but what about the angle? My question is related to angle calculation. Why is Y component is equal to the angle to rotate?
wdym, cframe.angle takes in several vectors to define itself, buildin up a 3x3 matrix
well, you can see in Cleversource’s algorithm that the yaw angle was calculated by the Y component of the cross product which are equal to each other. Why is this the case?
cframes are a 4x4 lookat matrix but we can only access the non homogenous portion so thats where the 3x3 comes from. Remember they are unit vectors so it is gonna just be some value on the unit circle aka radians aka angle
For this explanation, I will be working in 2D (because it’s easier). The same principles apply to 3D though.
-
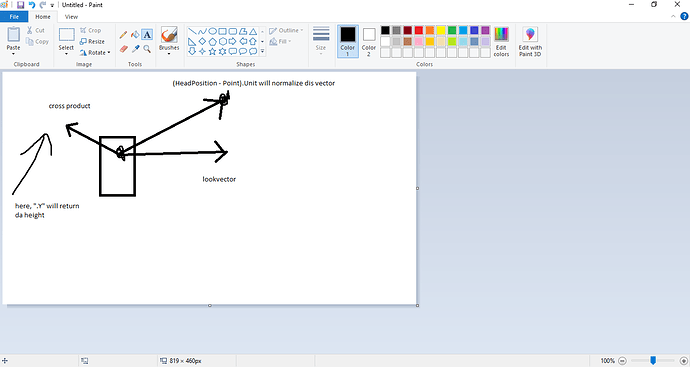
(HeadPosition - Point)
Get HeadPosition relative to the point.
Imagine drawing an arrow from the Point to the HeadPosition:

and then moving that arrow to the centre of the world.

-
(HeadPosition - Point).Unit
Now, imagine shrinking that arrow down so its length is just 1.

-
((HeadPosition - Point).Unit):Cross(TorsoLookVector)
Now get the cross product of this vector and whateverTorsoLookVectoris.
But hold on, what is a cross product?
A cross product is defined by a vector that is perpendicular to two vectors.

from Wikipedia
I don’t actually know why this works. Maybe you can do more research.
woah wat app r u usin to make these
I literally just used app.diagrams.net. It was a bit of a pain though.
well can you explain it further, i feel that you really understand what i’m saying but i really need a better explanation to visualize it, please
The length aka y value of a cross product is the area or in other words how much the vectors you multiplied it by relate, the area of the parallelogram they form. You are getting the cross product of 2 unit vectors. What this means is the max this length can be is 1, when they are at 90 degrees cause a square is base*height, 1 x 1 = 1. However you actually get a null vector (a vector with no magnitude) when they are facing parrallel to each other. Look lets just get rid of all this math jargin behind, it is basically the opposite of a dot product angle calculation. If you used a dot product for this when they are orthogonal you would get 1 or -1, in this you get 0 and vis versa. That *1 is probably to get rid of floating point errors I heard somewhere a while ago it somehow magically fixes them in lua
I forgot to mention this makes no sense in your case if you dont get this value and do math.deg(math.acos(value)) where value is your y thing
ok but that is quite confused, i don’t mean to offend you but it just makes no sense at all. It is not relevant to the question? WDYM by the opposite of a dot product angle calculation? Can you pls explain it more?
So you’re talking about how vectors define CFrame.Angle. SOrry because i misread it at first? Can you pls explain it further what is going on?