Why is n^0.5 faster than math.sqrt(n) and could it be faster?

C_Corpze · July 4, 2024, 9:45am

I’ve been doing a bunch of tests involving getting square roots for numbers, just a little optimization thing I like doing.

And I came upon these unusual results.

local iterations = 1_000_000



function sqrt(n)
	return math.sqrt(n)
end


function fast_sqrt(n)
	return n ^ .5
end


local sqrt_time      = 0
local fast_sqrt_time = 0



warn("== Normal sqrt ==")

math.randomseed(os.time())

local start_time = tick()
local result = 0


for i = 1, iterations do
	result = sqrt(math.random(1, 1_000_000))
end


sqrt_time = tick() - start_time
warn("sqrt time: \n", sqrt_time)




warn("== Potentially faster sqrt ==")

math.randomseed(os.time())

local start_time = tick()
local result = 0


for i = 1, iterations do
	result = fast_sqrt(math.random(1, 1_000_000))
end


fast_sqrt_time = tick() - start_time
warn("n^0.5 time: \n", fast_sqrt_time)



if fast_sqrt_time < sqrt_time then
	print("fast_sqrt was faster!")
else
	print("sqrt was faster!")
end

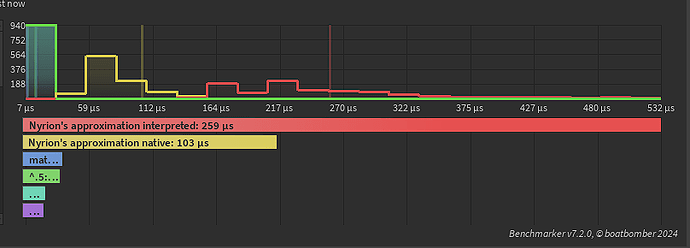
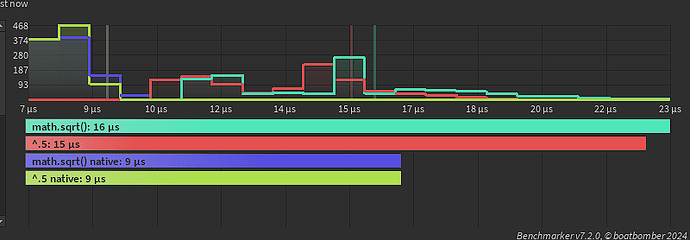
Well aware that this might not be the best way to test performance but here are my results, I don’t know if this might differ from processor to processor.

I tested this on an old laptop with a i7 7th gen, 4 cores and 16gb ram.

 11:22:55.104  == Normal sqrt ==
 11:22:55.176  sqrt time: 0.07180571556091309

 11:22:55.177  == Potentially faster sqrt ==
 11:22:55.229  n^0.5 time: 0.05223536491394043

 11:22:55.229  fast_sqrt was faster!

This should be 1 million iterations and the random seed is changed with each so that the results vary enough to hopefully not trigger some Luau optimizations / code folding.

Now, what could cause such a difference in speed?
I should include that math.sqrt(n) sometimes is still faster than n ^ 0.5 but on average it seems that n ^ 0.5 is slightly faster by some micro- or nanoseconds even though both give the same results, I haven’t noticed any loss in accuracy.

But could it be even faster?

This I’ve also been wondering.
There exists the Fast Inverse Square Root algorithm which was used in Quake I believe.

But this algorithm uses bit-shifting and whatnot and probably wouldn’t be as effective in Luau because it’s interpreted.

I wouldn’t mind some loss in accuracy in exchange for more performance.
If there’s a way to do even faster square roots in Luau it would be awesome.

Why would I want to do this?

Honestly, finding ways to make code fast and efficient is just one of my hobbies I guess.

I’m writing a library and I intend to have some module scripts that all contain optimized / faster / easier alternatives to commonly used functions that I will also end up using myself.

Hopefully Roblox makes native Luau work on the client too soon, but until then I’ll have to do with what’s currenlty possible in Luau and live games.

NyrionDev · July 4, 2024, 2:57pm

Here’s my attempt of creating a square root approximator:

local function sqrt(x: number): number 
	local current, prev = x/2, 0
	local threshold = 0.1
	while math.abs(current-prev) > threshold do
		prev, current = current, x/(current*2)+current/2
	end
	return current
end

Although it’s 30 times slower than the actual built-in function, I’m not sure if it can be optimized.

Another idea that came to mind was using the Magnitude property of vectors, basically for Vector2’s it calculates sqrt(x^2+y^2) and for Vector3’s sqrt(x^2+y^2+z^2) so as long you’re able to figure out x, y, z values or x, y values that satisfy the condition x^2+y^2+z^2 = input you will be able to calculate the square root of said input by passing x, y, z inside the vector constructors.

Good luck with finding something faster than n^0.5

C_Corpze · July 4, 2024, 3:46pm

It’s an interpreted language we’re working with after all.
If this was C++ we could’ve done some silly bit or memory manipulation to get interesting results.

I get the feeling it’s barely possible or otherwise really hard to make a square root approximator in a language such as Luau that is actually faster.
I do appreciate the effort though.

Figuring out why n^0.5 often runs faster is another mystery on it’s own.
I think once we know that it might already be a step closer to knowing how the Luau VM works internally I suppose.

SpiritXmas1 · July 14, 2024, 10:21pm

You can gain a general idea on why the process is faster by looking at the instructions generated by the luau compiler.

For example, the following script

local X = 16;
local Y = math.sqrt(X);

generates an instruction listing of

[1] LOADK      R0 K0; 16 (int)
[2] GETGLOBAL  R2 K1; 'math' (str)
[3] GETTABLEKS R1 R2 K2; 'sqrt' (str)
[4] MOVE       R2 R0
[5] CALL       R1 01 01
[6] RETURN     R0 0

To break down the instructions, the VM first loads the constant 16 into position 0 of the stack. It then grabs a global and stores it in position 2 of stack (this is the math library). The next opcode GETTABLEKS is of type iABC, meaning it uses all three registers. The first one is the result stack position, the second is the table and the third is the constant index. It indexes the table and stores the result in stack[1]. Some pseudo code to visualise this would look like the following

stack[1] = stack[2][constants[2]] -- local x = math["sqrt"]

The next two instructions prep the function call by moving the variable on top of the function and then calls it.

In comparison to this, the following script

local X = 16;
local Y = X ^ 0.5;

generates an instruction listing of

[1] LOADK  R0 K0; 16 (int)
[2] LOADK  R2 K1; 0.5 (int)
[3] POW    R1 R0 R2
[4] RETURN R0 0

Already by first glance you can tell the instruction listing is shorter and requires a lot less overhead. In addition to this, unlike the slower counterpart, this version of finding the square root doesn’t require any calls or get globals which would drastically improve performance (noticeable in high loads).

Also just to note, if you want to optimize the top example I recommend defining math.sqrt in a variable outside of your main loop.

Judgy_Oreo · July 14, 2024, 11:19pm

I think this is going a little too far into micro-optimization territory. Do you actually need to take the squareroot of a number millions of times a frame? I don’t think it’s worth the sacrifice to readability for most people.

SpiritXmas1 · July 14, 2024, 11:53pm

I don’t believe you sacrifice any readability, and on the contrary i think it is a good habit to cache your commonly used global functions. Not only does it improve performance over the whole script (which does become noticeable depending on script size), but it can also help with readability.

For instance instead of having math.sqrt referenced everywhere you can have a local variable defined at the top of the script local sqrt = math.sqrt; which in my opinion looks cleaner and would improve performance.

RoBoPoJu · July 15, 2024, 9:41am

I thought there was no need to do this anymore for built-in library functions due to the “Importing global access chains” optimization:

Is creating local variables for these functions still faster regardless of this optimization?

Prototrode · July 15, 2024, 11:14pm

There’s a performance difference in interpreting the code because math.sqrt is a function call.

If you enable native codegen (using either the --!native directive or the @native function attribute), you will discover that they have the pretty much the same performance. This is because in assembly they both mean the same thing.

By enabling native codegen

Benchmarks:

Benchmark code:

local a: number = 0

@native local function sqrtApproxNative(x: number): number 
	local current, prev = x/2, 0
	local threshold = 0.1
	while math.abs(current-prev) > threshold do
		prev, current = current, x/(current*2)+current/2
	end
	return current
end

local function sqrtApproxInterpreted(x: number): number 
	local current, prev = x/2, 0
	local threshold = 0.1
	while math.abs(current-prev) > threshold do
		prev, current = current, x/(current*2)+current/2
	end
	return current
end

return {
	ParameterGenerator = function()end,

	Functions = {
		['math.sqrt()'] = function()
			for i = 1, 1e3 do
				a = math.sqrt(i)
			end
		end,

		['^.5'] = function()
			for i = 1, 1e3 do
				a = i^.5
			end
		end,
		
		['math.sqrt() native'] = @native function()
			for i = 1, 1e3 do
				a = math.sqrt(i)
			end
		end,

		['^.5 native'] = @native function()
			for i = 1, 1e3 do
				a = i^.5
			end
		end,
		
		---[[
		["Nyrion's approximation native"] = function()
			for i = 1, 1e3 do
				a = sqrtApproxNative(i)
			end
		end,
		
		["Nyrion's approximation interpreted"] = function()
			for i = 1, 1e3 do
				a = sqrtApproxInterpreted(i)
			end
		end,
		--]]
	},
}

SpiritXmas1 · July 15, 2024, 11:29pm

Yes that is true, as long as the Luau compiler considers your environment “pure” it will automatically resolve the global table indexes at compilation. An environment is automatically considered “pure” as long as you do not use any of the following functions loadstring, setfenv and getfenv. What the IGAC optimization actually does is replace the indexing of the function from the table and the call with their own custom Luau opcodes, FASTCALL and GETIMPORT.

An example of this optimization can be show below, the script used for the example will be

local sqrtOf16 = math.sqrt(16)

Compiling with an optimization level of 0 provides us with this listing

[1] GETGLOBAL  R1 K0; 'math'
[2] GETTABLEKS R0 R1 K1; 'sqrt'
[3] LOADK      R1 K2; 16
[4] CALL       R0 1 1
[5] RETURN     R0 0

which is essentially a 1:1 match of standard Lua. Whereas when we compile with an optimization level of 1 we will see the usage of Luau’s custom opcodes.

[1] LOADN     R1 16
[2] FASTCALL1 25 R1 L0
[3] GETIMPORT R0 2; math.sqrt
[4] CALL      R0 1 1
[5] RETURN    R0 0

The usage of fastcall would considerably improve performance compared to the original listing, not only due to the indexing but also the usage of the custom FASTCALL opcode. Further benchmarking can be done on your local machine, but an old statistic by Roblox stated a SHA256 benchmark ran 1.75x faster.

thyswedishviking · July 15, 2024, 11:36pm

For the people who say this doesn’t matter, it really depends.

But for stuff like procedural generation, perlin noise, and randomness, especially on a large scale like terrain and part generation, it certainly matters.

Because having that increase in efficiency could allow for lower end devices to do more with less.
Of-course depending on use case.

C_Corpze · July 16, 2024, 4:39pm

A lot of interesting things I’m witnessing here.
In case you’re wondering, yeah I am working on an optimized code library.

But also, I might plan to use some quite intensive math functions and whatnot for visuals effects, NPC AI and other things that likely require thousands if not tens of thousands of iterations within a second.

Micro-optimizations might seem pointless, they sometimes are.
But I’d argue it’s valid if you’re planning to make use of things very intensively.

A while ago I was looking for a much faster way to compare distances really fast and figured it was faster to do if I wrote my own magnitude function and took out some of the square root operations since I only really need to know if object A is closer than object B.

But then I figured that I eventually might have to inevitably make use of square root somewhere anyways, so then I started looking for a way to do that faster.

If I code a bunch of AI-controlled NPCs in a game, it’ll only benefit everyone if I can make all of their thinking functions as fast as possible, this would allow me to have more active AI spawned and also program in some more intelligent behavior,
maybe even have zombies that can form strategies against the player for instance.

But that’s just scratching the surface.
I’m trying to learn as much about optimization as I can find.

Unfortunately a lot of C++ algorithms for instance aren’t very fast in Luau because there’s a huge difference between interpreted / natively compiled (and native code isn’t available on clients yet afaik, even if it was, Luau is not a low-level language so some operations still wouldn’t be fast).