Hello developers!!!
I saw that on Roblox there are some posts about Inverse Kinematics, but anyone explaining what or how it is done, so that’s what I come here for.
To understand this tutorial you will need a basic knowledge of vectors. If you don’t have it please check this post.
What is Inverse Kinematics?
Inverse Kinematics (IK) is a process that we are going to apply on a chain of bones to get them to position themselves in such a way that they reach a target point.
What does this mean? Imagine that I want to bring my arm from the shoulder to the target position:
How could we know what shape our arm has to take so that it can get to that position? By using the Inverse Kinematics.
There are many ways to do this, but the vast majority are too complicated and slow, but luckily, there is a much lighter and simpler method called FABRIK (Forward And Backward Reaching Inverse Kinematics).
This method has two parts: Backward and Forward:
Backward
The Backward method is the first of the two methods we are going to use, it consists of calculating the position of each of the bones from the last to the first one.
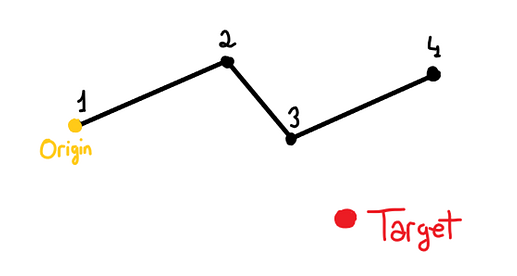
For a better understanding, I am going to do it as I explain it with this image here, which, as you can see, has a target position and a source position.
The first thing to do is to put the last bone in the same position as our target point and we will draw an imaginary line from the position of the new position of the last bone to the position of the penultimate bone and, on this line, we will put a point that is at the same distance as that between the last bone and the penultimate bone.
We will repeat this same process with all the stitches until we reach the first bone of all of them, with a result similar to this:
Forward
Once the first part of this algorithm is done, we can go to the second part, Forward, this part is quite similar to the previous one, it consists of putting the first bone in the origin position and, going forward instead of backward, do exactly the same as before but taking the new calculated bones as a reference.
For a better understanding, I will do with you the first one: let’s put the first bone again at the point of origin and let’s draw an imaginary line from this position to the position of the second bone that we calculated in the first step, NOT THE ONE WE HAD FROM THE BEGINNING and put a point on this line with the same distance from the first point as the one between the first point and the second one that we calculated in the first step:
We would be left with something similar to this:
How is this programmed?
Very good! Now that you understand everything, we can move on to programming.
In my case, I am going to use object oriented programming to make it more comfortable, in case you don’t know about it, here is a tutorial to help you understand the script.
We are going to create our first function to which we will need to pass an array with the parts that represent the bones, a number of iterations for a loop that we will make later and a Vector3 that will be our target position.
local IK = {}
IK.__index = IK
function IK.new(bones solverIterations, targetPosition)
end
return IK
Here, we are going to create an array and inside we are going to put the distance between the bones as follows:
function IK.new(bones, solverIterations targetPosition)
local bonesLenght = {}
for i = 1, #bones do
if i >= #bones then
bonesLenght[i] = 0
else
bonesLenght[i] = (bones[i].Position - bones[i + 1].Position).Magnitude
end
end
end
And to finish the function we are going to return a metatable with all the extracted information:
function IK.new(bones, solverIterations targetPosition)
local bonesLenght = {}
for i = 1, #bones do
if i >= #bones then
bonesLenght[i] = 0
else
bonesLenght[i] = (bones[i].Position - bones[i + 1].Position).Magnitude
end
end
setmetatable(
{
bones = bones;
solverIterations = solverIterations;
targetPosition = targetPosition;
bonesLenght = bonesLenght;
}, IK
)
end
Now we are going to create three more functions, one for the backward part, one for the forward part, one for the forward part and one to execute these functions more easily.
To the backward and forward functions, we will need to pass a parameter that is an array of vectors:
function IK:backward(forwardPosition)
end
function IK:forward(inversePosition)
end
function IK:solve()
end
We are going to start with the backward function, we are going to create an empty array that we are going to give vectors and we are going to return it at the end of the function.
function IK:backward(forwardPosition)
local inversePosition = {}
return inversePosition
end
Now let’s create an array that runs through all bones from back to front:
function IK:backward(forwardPosition)
local inversePosition = {}
for i = #forwardPosition, 1, -1 do
end
return inversePosition
end
Let’s stop here for a moment to analyze a little bit the formula we are going to use, which is this one here:
NextPosition + ((ActualPosition - NextPosition).Unit * Lenght)
When we subtract two vectors, we are obtaining another vector whose magnitude corresponds to the distance between the tips of the two subtracted vectors and in the direction between the tips of those vectors, as follows:
But as you can see, we obtain a vector that goes from the point (0, 0) towards the direction that I said before, but… we need it to start at the point P1 instead of at the point (0, 0), for this, we simply add the vector P1 to the subtraction, in this way we get the expected result:
Here we have a problem, we are going to use the last bone for the example, and it is that it will stretch the arm to always reach the target point, which we do not want, to solve it, we will normalize the vector of the subtraction and multiply it by the length that we calculate in the new function:
We are going to pass it to the code in this way:
function IK:backward(forwardPosition)
local inversePosition = {}
for i = #forwardPosition, 1, -1 do
local positionNext = inversePosition[i + 1]
inversePosition[i] = positionNext+ ((forwardPosition[i] - positionNext).Unit * self.bonesLenght[i])
end
return inversePosition
end
REMEMBER that we have to put the last bone in the target position, so it’s as easy as this:
function IK:backward(forwardPosition)
local inversePosition = {}
for i = #forwardPosition, 1, -1 do
if i == #forwardPosition then
inversePosition[i] = self.targetPosition.Position
else
local positionNext = inversePosition[i + 1]
inversePosition[i] = positionNext + ((forwardPosition[i] - positionNext).Unit * self.bonesLenght[i])
end
end
return inversePosition
end
For the forward function it is practically the same, the only difference is that instead of going from back to front, we go from front to back:
function IK:forward(inversePosition)
local forwardPosition = {}
for i = 1, #inversePosition do
if i == 1 then
forwardPosition[i] = self.bones[1].Position
else
local positionPrevious = forwardPosition[i - 1]
forwardPosition[i] = positionPrevious + ((inversePosition[i] - positionPrevious).Unit * self.bonesLenght[i - 1])
end
end
return forwardPosition
end
Perfect! We almost have it! It only remains to program the solve function, for it, we are going to create an array that has the position of the bones without making them any calculation:
function IK:solve()
local finalBonesPosition = {}
for i = 1, #self.bones do
finalBonesPosition[i] = self.bones[i].Position
end
end
We are going to change this array by the array that the forward function gives us when we pass the result of the backward function of this same array:
function IK:solve()
local finalBonesPosition = {}
for i = 1, #self.bones do
finalBonesPosition[i] = self.bones[i].Position
end
finalBonesPosition = self:forward(self:backward(finalBonesPosition))
end
Here if we want we can put it in another for loop that repeats as many times as we want:
function IK:solve()
local finalBonesPosition = {}
for i = 1, #self.bones do
finalBonesPosition[i] = self.bones[i].Position
end
for i = 1, self.solverIterations do
finalBonesPosition = self:forward(self:backward(finalBonesPosition))
end
end
And now all that remains is to apply the positions we obtained to their corresponding bone:
function IK:solve()
local finalBonesPosition = {}
for i = 1, #self.bones do
finalBonesPosition[i] = self.bones[i].Position
end
for i = 1, self.solverIterations do
finalBonesPosition = self:forward(self:backward(finalBonesPosition))
end
for i = 1, #self.bones do
self.bones[i].Position = finalBonesPosition[i]
end
end
We already have the ModuleScript finished! Here is the complete script so that you can read it without the explanations getting in the way:
Complete script
local IK = {}
IK.__index = IK
function IK.new(bones, solverIterations, targetPosition)
local bonesLenght = {}
for i = 1, #bones do
if i >= #bones then
bonesLenght[i] = 0
else
bonesLenght[i] = (bones[i].Position - bones[i + 1].Position).Magnitude
end
end
return setmetatable(
{
bones = bones;
solverIterations = solverIterations;
targetPosition = targetPosition;
bonesLenght = bonesLenght;
},
IK
)
end
function IK:backward(forwardPosition)
local inversePosition = {}
for i = #forwardPosition, 1, -1 do
if i == #forwardPosition then
inversePosition[i] = self.targetPosition.Position
else
local positionNext = inversePosition[i + 1]
inversePosition[i] = positionNext + ((forwardPosition[i] - positionNext).Unit * self.bonesLenght[i])
end
end
return inversePosition
end
function IK:forward(inversePosition)
local forwardPosition = {}
for i = 1, #inversePosition do
if i == 1 then
forwardPosition[i] = self.bones[1].Position
else
local positionPrevious = forwardPosition[i - 1]
forwardPosition[i] = positionPrevious + ((inversePosition[i] - positionPrevious).Unit * self.bonesLenght[i - 1])
end
end
return forwardPosition
end
function IK:solve()
local finalBonesPosition = {}
for i = 1, #self.bones do
finalBonesPosition[i] = self.bones[i].Position
end
for i = 1, self.solverIterations do
finalBonesPosition = self:forward(self:backward(finalBonesPosition))
end
for i = 1, #self.bones do
self.bones[i].Position = finalBonesPosition[i]
end
end
return IK
To finish definitively, we are going to create another script and execute the functions, but first we need to create the bones, in my case, I am going to put five bones, but you can do more or less:
We will also create a part for the target position:

Now let’s go to the scipt, let’s get the ModuleScript and execute the .new() function:
local bones = workspace:WaitForChild('Bones'):GetChildren()
local target = workspace:WaitForChild('Target')
local ikModule = require(game:GetService('ReplicatedStorage'):WaitForChild('IK'))
local ik = ikModule.new(bones, 4, target.Position)
Be careful with the array of bones! They have to be in the right order, otherwise, it will not work as we have in mind.
Now we are going to execute whenever we need to update the ik, we are going to execute the function ik:solve(), in this case, to save code since it is only a test, we are going to put it in a loop:
local bones = workspace:WaitForChild('Bones'):GetChildren()
local target = workspace:WaitForChild('Target')
local ikModule = require(game:GetService('ReplicatedStorage'):WaitForChild('IK'))
local ik = ikModule.new(bones, 4, target.Position)
local runService = game:GetService('RunService')
while true do
ik:solve()
runService.Heartbeat:Wait()
end
We will also need to create parts that start at one point and end at another to be able to visualize the system well, for that we will create a function something like this:
local segmentsFolder = workspace:WaitForChild('Segments')
local function drawSegment(start, target)
local part = Instance.new('Part')
part.Size = Vector3.new(.5, .5, (start - target).Magnitude)
part.CFrame = CFrame.lookAt((start + target) * .5, target)
part.BrickColor = BrickColor.Yellow()
part.CanCollide = false
part.Anchored = true
part.CastShadow = false
part.BottomSurface = Enum.SurfaceType.Smooth
part.TopSurface = Enum.SurfaceType.Smooth
part.Parent = segmentsFolder
end
And we apply the function to the loop:
while true do
ik:solve()
for i = 1, #bones - 1 do
drawSegment(bones[i].Position, bones[i + 1].Position)
end
runService.Heartbeat:Wait()
segmentsFolder:ClearAllChildren()
end
And… Finished!!! Time to see how the result looks like: IK Test Review
Complete script
local bones = workspace:WaitForChild('Bones'):GetChildren()
local target = workspace:WaitForChild('Target')
local ikModule = require(game:GetService('ReplicatedStorage'):WaitForChild('IK'))
local ik = ikModule.new(bones, 4, target)
local segmentsFolder = workspace:WaitForChild('Segments')
local function drawSegment(start, target)
local part = Instance.new('Part')
part.Size = Vector3.new(.5, .5, (start - target).Magnitude)
part.CFrame = CFrame.lookAt((start + target) * .5, target)
part.BrickColor = BrickColor.Yellow()
part.CanCollide = false
part.Anchored = true
part.CastShadow = false
part.BottomSurface = Enum.SurfaceType.Smooth
part.TopSurface = Enum.SurfaceType.Smooth
part.Parent = segmentsFolder
end
local runService = game:GetService('RunService')
while true do
ik:solve()
for i = 1, #bones - 1 do
drawSegment(bones[i].Position, bones[i + 1].Position)
end
runService.Heartbeat:Wait()
segmentsFolder:ClearAllChildren()
end
The project can be downloaded here: IK.rbxl (38.0 KB)