Vector Mathematics 101 - Volume I
A Basic Course on Vectors

Preface
Vectors are a concept fundamental to dealing with spatial environments and, in our case, development on Roblox, but it is common to observe difficulties in grasping the ideas. It is the aim of this text to provide the intuition behind vectors and basic vector operations, and aid the reader in mathematical operations pertaining to vectors. It is assumed that the reader has basic knowledge of scripting.
The text will be divided into three major components - the conceptual, the applications and the proofs - which will be added with the passage of time in the order given. Note that for conceptual topics, excercises containing questions and challenges will be added at some point to examine knowledge retained and ability to apply vector mathematics to Roblox.
Chapter 1 -The Cartesian Plane
To realize what vectors are, we should first have a quick glance at something known as the Cartesian Plane, or more commonly referred to as the Coordinate Plane.
The image above is a Cartesian Plane, and is used to locate 2D positions. It consists of two number lines perpendicular to one another.
The horizontal line is called the X-Axis, while the vertical line is called the Y-Axis.
Positions on this plane are expressed using Ordered-Pairs / Coordinates, which are two-numbered lists where the first number denotes the number of steps moved along the X-Axis from the point where the X-Axis and the Y-Axis intersect, i.e the Origin, and the second denotes the number of steps moved along the Y-Axis from your current position on the X-Axis.
For example, the coordinate (1, 5) can be located by first moving 1 step to the right of the Origin, then moving 5 steps up.
Similarly, to find the location at (-7, -3), we must first move 7 steps to the left of the origin and 3 steps down. This is how 2D positions are located.
It is of interest to note the following:
IDEA
For any given coordinate, there exists only one matching location
For any given location, there exists only one matching coordinate
Now that we’ve dealt with coordinates, we can hop onto vectors. Please note that from here on-out, we will abandon the 2D plane in our analysis and instead refer to 3D space - not much will change besides the addition of a third number to coordinate lists and the introduction of depth.
Chapter 2 - Introduction to Vectors
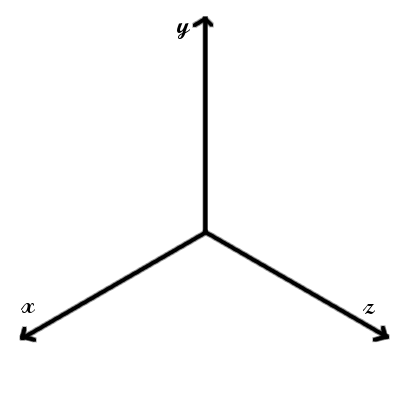
Now, the key thing about coordinates is that they refer to simple positions. Imagine a single dot in space - such a location is referred to as a coordinate.
How do vectors work, then?
Imagine moving from the Origin of 3D space onto the dot you imagined earlier.
Similarly, imagine moving from any random starting point to any random finishing point.
You see, your movement from one dot to the other is referred to as a Vector.
A more formal definition of the vector would be as follows:
DEFINITION
A Vector is a quantity that possesses magnitude and direction
What does this mean for us? You can place your vector anywhere, but the length of travel and the direction of travel are what distinguish each vector, hence if these two quantities are the same, then both vectors are the same.
How do we represent this motion and therefore our vectors? We do so using two ideas - names and bases.
In typical coordinate work, a coordinate is named with a single letter, e.g ‘X’.
When naming vectors, however, we’ll use a more elaborate naming convention - instead of a single letter, we’ll use two letters. The first letter represents the starting point of our movement, and the second letter represents the ending point of our movement.

We have two coordinates, ‘A’ and ‘B’. Our naming convention means the vector representing the movement from A to B will be named AB.
You can use any naming convention if you wish, but this convention will be used throughout the remainder of the text.
Next comes the idea of base vectors - this is how we’ll actually represent the numerics behind vectors.
What are base vectors? If you can recall, each number in a coordinate meant the number of steps in a particular direction taken along an axis. In mathematics, the idea of a step along an axis is referred to as a Base Vector.
We have three axes, hence we have three base vectors.
In mathematics, the base vector representing a single step in the direction of the X-Axis is denoted by ‘i’.
Similarly, the base vectors representing a single step in the directions of the Y-Axis and Z-Axis are denoted by ‘j’ and ‘k’ respectively.
Now onto a major idea regarding the base vectors:
IDEA
Any vector can be broken down into a combination of base vectors
So for instance, if the point X is at the coordinates (2, 3, 5), and the point Y is at (1, -3, 7), then the vector XY would be expressed as -i-6j+2k, which means you move 1 step in the opposite direction of the X-Axis, 6 steps in the opposite direction of the Y-Axis, and 2 steps in the direction of the Z-Axis.
IDEA
The vector represented by ai+bj+ck, where a, b and c are numbers, means that you move a steps along the X-Axis, b steps along the Y-Axis and c steps along the Z-Axis. If any coefficient of a base vector is negative, it means moving as many steps but in the opposite direction.
Since our intended usage is Roblox, it is of use to mention another idea:
IDEA
The vector represented by ai+bj+ck can be expressed in Roblox by Vector3.new(a, b, c)
Do note that Roblox handles the base vector business itself when you use Vector3.new(), but be careful to place the co-efficients of the base vectors in the correct order. It is also of interest to know that if a coefficient is 0, you can ignore it in both the math notation and Roblox’s Vector3 - for instance, the vector 2i+3k can be represented as Vector3.new(2, , 3). You could even put the zero in blank spaces, if you so wish. Anyhow, we’ll continue using math notation for now, but we’ll return to Roblox once all the fundamental ideas have been explained.
With that, we know have a basic understanding of vectors and can move onto fundamental vector operations. One major thing to note - we’ll be abandoning coordinates from now own. Instead, a position will be considered a vector going from the origin to the desired position - this is often called a Position Vector. An important point to note is that in our convention, a position vector will always start with the letter ‘O’. An example is that the vector moving from the Origin to X would be OX.
EXCERCISE 1
Q1 - Describe the vector represented by 5i+3j+7kQ2 - Describe the vector represented by 6j and express it in Vector3 form
Chapter 3 - Fundamental Vector Operations

We’ll use the figure above as a reference for our ideas in a short while.
A quick recap, we referred to a vector as a movement from a start to a finish.
This idea can be extended to explain the idea of adding two vectors.
Imagine three random points in 3D space, then name them ‘P’, ‘Q’ and ‘R’.
Now imagine moving from P to Q, then Q to R.
What’s interesting is that this movement is equivalent to moving directly from P to R. So if PQ and QR are vectors, then the combination of these two is equivalent to the vector PR. Thus the following idea:
IDEA
AC = AB + BC
But that’s not all. Remember how vectors could be expressed as a combination of base vectors?
Say you moved by 3 steps along the X-Axis, then moved 1 step in the opposite direction of the X-Axis from that point - this is equivalent to moving 2 steps in the direction of the X-Axis from the beginning.
The same principle applies to the rest of the base vectors as well, hence we can extend this idea even further:
IDEA
If AC = AB + BC, and if AB = ai+bj+ck and BC = pi+qj+rk, then
AC = (a+p)i+(b+q)j+(c+r)k
The idea described above is known as Vector Addition.
From this, we can also derive another idea.
Imagine a dot and moving to it from the origin - now imagine performing the same movement all over again, but starting from the dot instead.
We’re going to examine this idea through some abstract calculations:
CALCULATION
Let AB = ai+bj+ck
AB+AB = (a+a)i+(b+b)j+(c+c)k
2AB = (2a)i+(2b)j+(2c)k
Through this calculation, we have now realized the idea in question:
IDEA
If AB = ai+bj+ck
sAB = (sa)i+(sb)j+(sc)k
This is known as Vector Scaling.
This procedure preserves the direction of said vector while extending its length as many times as the scaling value, i.e a Scalar.
Since we’ve used the term ‘scalar’, it’s time to elaborate:
DEFINTION
A Scalar is a quantity possessing magnitude only
Interestingly though, the idea of scaling leads to something else as well:
IDEA
-AB = -ai-bj-ck
So scaling by a negative number will flip it, then extend its length.
So if a vector AB described moving from A to B, then multiplying it by -1 would cause it to end up describing the motion from B to A.
This naturally leads to another idea:
IDEA
-AB = BA
Now onto the diagram we have at the start of this section.
Do you notice the two green vectors, OA and OB?
It can be observed through the diagram and our previous statements that OA + AB = OB.
Through some algebraic manipulation, we can also observe the following:
IDEA
If OA + AB = OB, it can be re-arranged to attain AB = OB - OA, which can be further altered to acquire AB = -OA + OB, which is equivalent to AB = AO + OB
The vector AB is called a Relative Vector, since it describes the movement to B with respect to some point that isn’t the origin, which is usually treated as the most basic point of reference.
DEFINITION
A Relative Vector describes the movement from one position vector to the other
And with that, we’ve dealt with the more basic operations.
The next concept we’ll investigate is known as the magnitude.
DEFINITION
The magnitude of a vector refers to the distance between the starting point and finishing point
How would we compute the magnitude of a vector? We do so by looking back on something known as the Pythagorean theorem. First, let’s setup a diagram.

We’re going to calculate the magnitude of the vector OX and to do so will use the Pythagorean theorem. Here’s a quick recap on what that is:
EQUATION
In a right-angled triangle where the sides perpendicular to one another are ‘a’ and ‘b’, and the third line, the hypotenouse, is ‘c’, then a² + b² = c²
You may have seen this in Geometry or Algebra at some point. This equation is of great use to us in our current agenda.
Since vectors are akin to lines, we can subject them to such equations.
Take a quick glance at our diagram.
Let’s refer to the length of OX (3i+12j+4k) as ‘l’ for our purposes. When plugging in values from 3D space, we’ll omit the base vector letters because they are only meant to provide a sense of direction - the real deal is the co-efficient.
First, we must isolate two lines perpendicular to one another such that they form a triangle with l as the hypotenouse.
As you can see, the two lines we’re interested in are the 12j line and the green line. We’ll refer to that as ‘x’. We can imagine them in a 2D plane as so:

CALCULATION
l² = x² + 12²
Before we can find l, we must first find x. To do so, we’ll setup another equation such that x can be calculated.
If you look at the original diagram, you’ll notice that 3i and 4k form a right-angled triangle with x as the hypotenouse. This is precisely what we needed.

We can now calculate x using the Pythagorean theorem.
CALCULATION
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √(25)
x = 5
The value of x is 5. Now that we have x, we can plug it in our original equation to find l.
CALCULATION
l² = x² + 12²
l² = 5² + 12²
l² = 25 + 144
l² = 169
l = √(169)
l = 13
And with that, we’ve found the length of l. However, something of interest is that instead of having to use the equation twice, our calculations show that it is possible to jump to the final calculation directly.
CALCULATION
l² = x² + 12² and x² = 3² + 4², hence
l² = 3² + 4² + 12²
l² = 9 + 16 + 144
l² = 169
l = √(169)
l = 13
Thus we can conclude the following:
IDEA
If AB = ai+bj+ck, then
|AB| = √(a²+b²+c²)
Something to note - if a vector is inside two | characters, then it represents the magnitude of said vector.
Something else we must note however is that AB is a relative vector - usually, we find magnitudes using position vectors, therefore we must modify our conclusion to take that into account
IDEA
If OA = ai+bj+ck and OB = pi+qj+rk, then
|AB| = √((p-a)²+(q-b)²+(r-c)²)
And finally, this idea can be further abstracted as so:
IDEA
|AB| = √((Δx)²+(Δy)²+(Δz)²)
Where ‘Δ’ (Pronounced: Delta) means ‘change in’. The reason for the usage of change is that when you have two position vectors, you derive the distance between the two through the relative vector, and the components of the relative vector equals the change or difference between the components of the two vectors.
Now that we’ve examined magnitudes, there remains only one more concept that we’ll tackle at present - Unit Vectors
What are unit vectors? Well, to understand them, we’ll first take a quick look at how quantities in real life work.
When you say something like “5 meters”, what you mean is 5 times the standard meter unit.
Similarly, when you say something like “12 kilograms”, what you mean is 12 times the standard kilogram unit.
The number means nothing on its own - it is paired with a unit of some kind to make sense.
So, essentially, any quantity would work as follows:
IDEA
Physical Quantity = Magnitude * Unit
With that, we can lay down the definition of a unit vector
DEFINITION
The Unit Vector of a given vector is such that it has the same sense of direction but has a magnitude equal to 1
So say for instance we have some vector, AB. The unit vector of AB would have the same direction of movement as AB, but would be a length equal to a single step in the direction of AB.
What’s interesting to note is that this idea of unit vectors leads to a revelation:
IDEA
The base vectors i, j and k are unit vectors
So, how do we find the unit vector? To do so, we’ll first algebraically manipulate the idea of the physical quantity
IDEA
If Physical Quantity = Magnitude * Unit, then Unit = Physical Quantity / Magnitude
So to get the unit of something, we must divide it by its magnitude. Therefore, to find the unit of a vector, we must divide the vector by its own magnitude.
IDEA
If AB = ai+bj+ck, then its magnitude, |AB|, can be found by √(a²+b²+c²), and since sAB = (sa)i+(sb)j+(sc)k, then the unit of the vector in the direction of AB is (1/|AB|)(AB), and (1/|AB|)(AB) = (a/|AB|)i+(b/|AB|)j+(c/|AB|)k
What use does the unit vector have? Well, say you already have a relative vector or a Direction Vector
DEFINITION
A Direction Vector describes the direction of movement from a starting point to a finishing point - it is calculated the same way as a relative vector
If you have such a vector, then you can scale it however you wish and the direction of travel remains the same, but the magnitude had to be calculated repeatedly if needed. But if the direction vector is a unit vector, then by the principle of vector scaling, the scalar value multiplying a unit direction vector equals the magnitude of the resulting vector
IDEA
If AB is a unit vector, then |kAB| = k
This idea will prove very useful once we deal with abstract lines in 3D space.
Well, that’s how you’d approach the basic operations regarding vectors in mathematics. Now that you have a grasp of the ideas, we’ll summarize how to approach said concepts with Roblox.
--For Vector Addition,
local ResultantVector = VectorA + VectorB
--For Scaling,
local ResultantVector = (ScalarValue)*(Vector)
--For finding the relative vector,
local ResultantVector = VectorB - VectorA
--For finding the magnitude of an ordinary vector,
local Length = Vector.Magnitude
--For finding the magnitude of a relative vector,
local Distance = (VectorB - VectorA).Magnitude
--For finding the unit vector of an ordinary vector,
local UnitVector = Vector.Unit
--For finding the unit vector of a relative vector or a direction vector,
local UnitVector = (VectorB - VectorA).Unit
Now that we’ve covered vector addition, scaling and magnitudes, we will investigate something often feared - the Dot Product!
EXCERCISE 2
Q1 - Describe the result of adding 2i+5k and 7i+3jQ2 - Given that A = 9i+3j+12k and B = 4i+8j+k, find
(i) The result of A+B
(ii) The result of A-B
(iii) The result of B-A
(iv) The result of -A-BQ3* - Given that a set of vectors can be arranged to make a closed polygon, what can you deduce about the set of vectors?
Q4 - Compare kX with -kX - how do they differ? What is the signifance of k if X is a unit vector?
Q5 - Given A and B from Q2, find
(i) 3A+2B
(ii) 5B-4AQ6 - Find the length of the vector represented by 2i+4j+3k, and hence give the unit vector both along and opposite to this vector.
Q7 - The point A rests at (4, 1, 3) whilst B and C lie on (2, 5, 1) and (3, -2, 4) respectively. Find all the distances between the points, and state the shortest such distance.
Chapter 4 - Dot Products
Note that from this section, knowledge of Trigonometry is assumed. A separate, and more in-depth guide on Trigonometry will be uploaded in due time.
Now, we’ve defined the addition of vectors as well as the multiplication of a vector and a scalar. The question on our minds now is how multiplication of vectors would work, and what would the product mean.
If we multiplied two vectors together, we’d have two possibilities to choose from - scalars and vectors. The case where the output is a scalar is known as the Dot Product, and it has a rather interesting meaning behind it.
Suppose there exist two vectors in space, p and q, that lie on the same plane (In-fact, any two vectors always lie on a common plane) as so

Would you agree that there is a vector along q, p’, that covers as much distance along q as p?

Well, the product of |p’| and |q| is the dot product!
A more formal definition is as follows
DEFINITION
The dot product of two vectors, a and b, is defined as the magnitude of the projection of a onto b multiplied by the magnitude of b itself
a.b = |a’||b|
If they lie on the same plane, then surely there is an angle between the two vectors, right?

If you’ve tackled Trigonometry before, you might realize that |p’| is really just |p|Cos(Ɵ)
And we can now update our former equation as so
EQUATION
a.b = |a||b|Cos(Ɵ)
There’s something else to discover too! By looking at the equation, you realize that the order of the vectors in the dot product doesn’t matter!
The equation we saw is but one method of calculating the dot product. The other method is as so
EQUATION
If a = xi+yj+zk and b = pi+qj+rk, then
a.b = xp+yq+zr
We’ll delve into why this method works much later once we establish a solid grasp on space.
If the two equal the same thing, then by principles
EQUATION
If a = xi +yj +zk and b = pi +qj +rk, and there is an angle Ɵ between a and b, then
a.b = xp+yq+zr
and
a.b = |a||b|Cos(Ɵ)
hence
xp+yq+zr = |a||b|Cos(Ɵ)
You can actually use that nifty equation to find the angle between vectors!
Some interesting properties to note though
IDEA
If the angle between a and b is acute, then a.b > 0
If a and b are perpendicular, then a.b = 0
If the angle between a and b is obtuse, then a.b < 0
The maximum value of a.b occurs when Ɵ = 0°
That’s really all there is to the dot product!
Why do those properties work? Finding that will be up to you for this one!
Next up, we’ll analyze line equations. But before we do, here’s the Dot Product as it would be expressed in Roblox.
--For finding the DotProduct given two vectors,
local DotProduct = VectorA:Dot(VectorB)
--For finding the DotProduct given two magnitudes and an angle,
local DotProduct = VectorA.Magnitude * VectorB.Magnitude * math.cos(Angle)
--For finding the angle between two vectors,
local Angle = math.acos(VectorA:Dot(VectorB)/(VectorA.Magnitude * VectorB.Magnitude))
EXCERCISE 3
Q1 - Find the Dot Product of 5i+6k and 3j+4kQ2 - Determine if 5i+12j+13k and 3i+4j+5k are perpendicular or not
Q3 - Explain why the Dot Product is maximal when Ɵ = 0°
Chapter 5 - Constructing Lines
When dealing with vectors, we often want to deal with unrestricted lines. If you noticed, the vectors we have been discussing are finite, i.e limited. How would we introduce unrestricted lines to the world of vectors?
To answer that question, we first need to determine what do we need to describe a line.
Lines have an infinite number of possible directions - rotating or changing the direction of the line by even a tiny nudge can completely change it. Hence, we can be certain that the direction of a line is necessary to describe it.
Lines can also have an infinite number of positions - but what does position mean in this context?
In our case, if we grab a line at some arbitrary point on it and then carefully move the line without changing its rotation, we have generated a new line. As a result, we have also realized that the position of a line is also necessary to describe it.
There are no further properties we need to take into account to describe a line, hence we can now get onto their construction.
You might recall seeing this old beast somewhere before
EQUATION
f(x) = mx+c
y = mx+c
If you do, you might also recall how it works. In a nutshell, the m describes the line’s direction while the c describes its position. But just what exactly is x? In this case, x happens to be the horizontal coordinate of any point along the line.
This idea actually ends up being used to construct vector lines, but note that the terms themselves mean different things in this new context.
EQUATION
If we have the Direction Vector of a line, d, and some arbitrary Position Vector p which is contained in the line, then the line is represented by the equation
r = p+λd
where r denotes the Position Vector of a point on the line and λ is a variable or parameter
For the sake of tying this in neatly with the concept of functions, allow me to restate the given equation.
EQUATION
r(λ) = p+λd
where r(λ) denotes the Position Vector of a point on the line for a particular value of the parameter λ
EXAMPLE
r(λ) = (2i+3j+5k)+λ(7i+3k)
r(λ) = (2+7λ)i+3j+(5+3λ)k
If you recall our earlier discussion on Unit Vectors and Vector Scaling, you might be able to realize that the equation can gain a new meaning in a very special case
IDEA
In r(λ) = p+λd, λ represents the distance of r(λ) from p if d is a Unit Vector
That is pretty much all there is to constructing lines. Or is there?
Well on Roblox, you also have Raycasting. It deals with the same idea - shooting lines given an origin and a direction - but it does so mainly to figure out if there are any objects interfering along this path.
local Ray = Ray.new(Origin, Direction)
The Origin refers to the Vector3 of our line’s reference point p whilst Direction refers to the Vector3 of our Direction Vector d.
In a nutshell, a Raycast shoots an imaginary line and tells you if something hit it and in such case, where the hit occurred. You’d use this for Physics or spatial analysis more-so than moving an entity along a line as we wish to, so we’ll brush it aside now.
Chapter 6 - Introduction to Vector Functions
Funnily enough, our ideas can actually be generalized further. Let’s take our line equation and do some crunching on it.
r(λ) = p + λd
Let p = ai+bj+ck and d = xi+yj+zk
r(λ) = ai+bj+ck + λ(xi+yj+zk)
r(λ) = (a+xλ)i+(b+yλ)j+(b+zλ)k
Now observe - the key step
r(λ) = f(λ)i + g(λ)j + h(λ)k
where f(λ) = a + xλ, g(λ) = b + yλ and h(λ) = c + zλ
We’ve now realized that each individual component can be expressed as a classic function in terms of λ multiplying with the unit vectors!
The real kicker, however, is this bit - the functions we made need not exist in that form! The key to abstracting this idea lay in generalizing the functions of λ!
The only reason our functions of λ ended up being linear was because of the fact that we started off with vector lines - however, this isn’t necessary any further. Whilst we went from line to function - the idea truly goes from function to line.
Let’s take a brief detour and take a look at a more concrete example of a vector function - projectiles!
There will be no exercise for this portion - instead, the bulk of exercises on this will be carried by the Projectile Motion and Tangential Vector chapters.
Chapter 7 - Projectile Motion I
If you’ve ever tackled Physics / Mechanics, you may recall these equations from your studies
The Equation of Motion for Constant Velocity
v = s/t
The Equations of Motion for Constant Acceleration
v = u + at
s = ut + at²/2
v² = u² + 2as
Where v is the velocity, u is the initial / starting velocity, s is displacement and a is acceleration. The derivation of these equations can be achieved by assuming constant acceleration and applying knowledge of Calculus, but we will not tackle that here.
Now to get closer to our goal of projectiles, we need to recall the idea of Gravity.
DEFINITION
Gravity is a phenomena which pulls bodies towards one another
In the context of Roblox and our own simplistic observations however, Gravity is rather simple - it is the phenomena that brings bodies downwards.
To numerically implement gravity, we must introduce the acceleration due to gravity, which is often denoted by g. You may have dealt with this in Physics / Mechanics and ascribed to it values such as 10 m/s² or 9.8 m/s². Roblox’s gravity is set to 196.2 studs/s² - the number being a consequence of the internal conversion of meters to studs. Note that using gravity like this assumes constant gravitational acceleration - an assumption often made when dealing with near-surface interactions.
The simplest body we should examine before heading to the projectile is that of a dropped object - we shall apply the equations of motion on this case immediately.
SCENARIO
Jack drops a stone from the top of a 50m building. How long does it take for the stone to reach the bottom, and how fast is the stone when it reaches the middle of the building?
CALCULATIONS
Facts we know:
As g is almost constant at the surface of the earth, we shall assume that throughout this motion g has a fixed value of 10m/s²
Because the stone was dropped and not thrown down, we know that u = 0m/s
Solving for time:
s = ut + at²/2
50 = 0t + 10t²/2
50 = 10t²/2
100 = 10t²
t² = 10 → t = √10 (3.162… seconds)
Solving for velocity:
v² = u² + 2as
v² = 0² + 2(10)(25)
v² = 500 → v = 10√5 (22.36… meters / second)
With that example done, we shall see the larger ideas of Projectile Motion arise in a Volume II.
Intents of Volume II
Conceptual
- Projectile Motion II
- Cross Products
- Planes in Space
- Polar and Spherical Coordinates
- Tangential Vectors
Applications
- Reflecting Lines
- Visualizing Functions
- Grid Placement
- Spherical System
List of Formulae
Magnitude
|v| = √(x² + y² + z²)
Dot Product
u.v = |u||v|Cos(Ɵ) = ax + by + cz
Vector Function of a Line
r(λ) = p + λd
The Equation of Motion for Constant Velocity
v = s/t
The Equations of Motion for Constant Acceleration
v = u + at
s = ut + at²/2
v² = u² + 2as
This text has been hence completed and will be carried on by Volume II - DM or reply in case of any errors or critiques
